
| A. | 576种 | B. | 504种 | C. | 288种 | D. | 252种 |
分析 把男生甲与女生乙排在一起作为一个元素,剩余3个男生与3个女生,按照男生、女生不相邻的插空排法共有${A}_{3}^{3}$•${A}_{4}^{3}$不同的站法;
再把男生甲与女生乙放入,符合条件的是$\frac{1}{2}$${A}_{7}^{1}$•${A}_{3}^{3}$•${A}_{4}^{3}$种不同的站法.
解答 解:4个男生4个女生站成一排,把男生甲与女生乙排在一起作为一个元素,
剩余3个男生与3个女生,按照男生、女生不相邻的插空排法,
有${A}_{3}^{3}$•${A}_{4}^{3}$=6×24=144种不同的站法;
现在有7个位置把男生甲与女生乙放入,符合条件的是:
$\frac{1}{2}$${A}_{7}^{1}$•${A}_{3}^{3}$•${A}_{4}^{3}$=$\frac{1}{2}$×7×144=504.
故选:B.
点评 本题考查了排列组合的综合运用问题,解题时应注意常见问题的处理方法,如相邻问题用捆绑法,不相邻问题用插空法等.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4} | B. | {2,4,5} | C. | {1,2,3,4} | D. | {1,2,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (-3,+∞) | C. | (-∞,3) | D. | (-∞,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
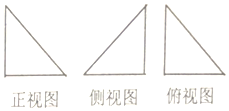 一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )
一几何体的三视图如图所示,三个三角形都是直角边为2的等腰直角三角形,该几何体的顶点都在球O上,球O的表面积为( )| A. | 16π | B. | 3π | C. | $4\sqrt{3}π$ | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com