
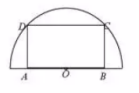
 如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、
如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、分析 (1)OA=2$\sqrt{4{0}^{2}-{x}^{2}}$=2$\sqrt{1600-{x}^{2}}$,可得y=f(x)=2x$\sqrt{1600-{x}^{2}}$,x∈(0,40).
(2)平方利用基本不等式的性质即可得出.
解答 解:(1)AB=2OA=2$\sqrt{4{0}^{2}-{x}^{2}}$=2$\sqrt{1600-{x}^{2}}$,
∴y=f(x)=2x$\sqrt{1600-{x}^{2}}$,x∈(0,40).
(2)y2=4x2(1600-x2)≤4×$(\frac{{x}^{2}+1600-{x}^{2}}{2})^{2}$=16002,即y≤1600,当且仅当x=20$\sqrt{2}$时取等号.
∴截取AD=20$\sqrt{2}$时,才能使矩形材料ABCD的面积最大,最大面积为1600.
点评 本题考查了函数的性质、矩形的面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{3}$) | B. | (-3,-1) | C. | (-1,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{x}-\frac{1}{y}>0$ | B. | ${(\frac{1}{2})^x}-{(\frac{1}{2})^y}<0$ | C. | log2x+log2y>0 | D. | sinx-siny>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com