
分析 判断函数的奇偶性,通过x大于0,判断函数是增函数,然后转化求解不等式的解集即可.
解答 解:函数f(x)=log2(2+|x|)-$\frac{1}{2+{x}^{2}}$,是偶函数,
当x≥0时,y=log2(2+x),y=-$\frac{1}{2+{x}^{2}}$都是增函数,所以f(x)=log2(2+x)-$\frac{1}{2+{x}^{2}}$,x≥0是增函数,
f(x-1)>f(2x),可得|x-1|>|2x|,可得3x2+2x-1<0,解得x∈(-1,$\frac{1}{3}$).
故答案为:(-1,$\frac{1}{3}$).
点评 本题考查函数的与方程的应用,函数的奇偶性以及函数的单调性的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36π | B. | 4π | C. | $\frac{27}{4}$π | D. | $\frac{27}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
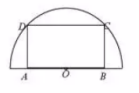 如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、
如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com