练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量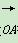＝(λcosα，λsinα)(λ≠0)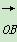，＝(－sinβ，cosβ)，其中O为坐标原点．

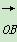    (1)若α－β＝且λ＝1，求向量与的夹角；

    (2)若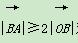对任意实数α，β都成立，求实数λ的取值范围．


    β都成立，即(λcosα＋sinβ)2＋(λsinα－cosβ)2≥4对任意实数α，β都成立．

    整理得λ2＋1＋2λsin(β－α)≥4对任意实数α，β都成立．

    因为－1≤sin(β－α)≤1，

    所以

    解得λ≥3或λ≤－3.

    所以实数λ的取值范围为(－∞，－3]∪[3，＋∞)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知△ABC的周长为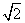＋1，且sinA＋sinB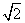＝sinC.若△ABC的面积为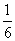sinC，则角C的大小为(　　)

    A．30°                                 B．60°

    C．90°                                 D．120°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


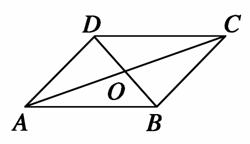
    如图，设O是平行四边形ABCD的两条对角线AC，BD的交点，下列向量组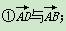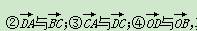：其中可作为这个平行四边形所在平面的一组基底的是(　　)

    A．①②                                 B．③④

    C．①③                                 D．①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点A(－1,1)，B(1,2)，C(－2，－1)，D(3,4)，则向量方向上的投影为(　　)

    A.                                 B.

    C．－                              D．－

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，平面四边形ABCD中，AB＝13，AC＝10，AD＝5，cos∠DAC＝，＝120.

    (1)求cos∠BAD；

    (2)设求x，y的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在复平面内，复数z1，z2对应的向量分别是，则|z1＋z2|＝(　　)

    A．2

    B．3

    C．2

    D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若z＝sinθ－＋i是纯虚数，则tan＝(　　)

    A．－                                 B．－7

    C．－                                 D．－1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，P是△ABC的∠ABC和∠ACB的外角的平分线的交点，若∠A=90°，则∠P=　　．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设{an}是公比为q的等比数列，则“q>1”是“{an}为递增数列”的(　　)

    A．充分而不必要条件

    B．必要而不充分条件

    C．充分必要条件

    D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案