
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 4 |
分析 由已知得P(0,b),$\overrightarrow{P{F}_{1}}$=(-1,-b),$\overrightarrow{P{F}_{2}}$=(1,-b),从而$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=b2-1=2,由此利用椭圆性质能求出a.
解答 解:∵F1(-1,0),F2(1,0)是椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,P为E的上顶点,
∴P(0,b),$\overrightarrow{P{F}_{1}}$=(-1,-b),$\overrightarrow{P{F}_{2}}$=(1,-b),
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=2,
∴$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=b2-1=2,
解得b2=3,∴a2=3+1=4,
解得a=2.
故选:B.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)≥2-4ln2 | B. | f(x)≤2-4ln2 | C. | f(x)≥4-8ln2 | D. | f(x)≤4-8ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
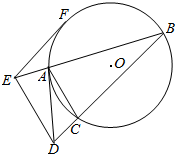 如图所示,△ABC内接于⊙O,直线AD与⊙O相切于点A,交BC的延长线于点D,过点D作DE∥CA交BA的延长线于点E.
如图所示,△ABC内接于⊙O,直线AD与⊙O相切于点A,交BC的延长线于点D,过点D作DE∥CA交BA的延长线于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<3} | B. | {x|-4<x<-2} | C. | {x|-4<x<2} | D. | {x|-2<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com