
(14分)如图,圆柱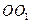 内有一个三棱柱
内有一个三棱柱 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱
底面的内接三角形,且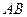 是圆
是圆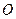 的直径。
的直径。
(I)证明:平面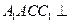 平面
平面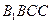 ;
;
(II)设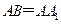 ,在圆
,在圆 柱
柱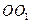 内随机选取一点,记该点取自三棱柱
内随机选取一点,记该点取自三棱柱 内的概率为
内的概率为 。
。
(i)当点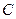 在圆周上运动时,求
在圆周上运动时,求 的最大值;
的最大值;
(ii)如果平面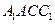 与平面
与平面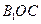 所成的角为
所成的角为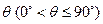 。当
。当 取最大值时,求
取最大值时,求
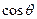 的值。
的值。
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且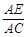 =
= =λ (0<λ<1).
=λ (0<λ<1).
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时?平面BEF⊥平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC— B。
B。
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E—DF—C的余弦值;
(3)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知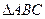 中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
(1)求证: AD⊥面SBC;
(2)求二面角A-SB-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若{a,b,c}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
| A.a,a+b,a-b | B.b,a+b,a-b |
| C.c,a+b,a-b | D.a+b,a-b,a+2b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com