
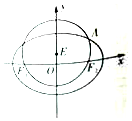
 如图,在平面直角坐标系xOy中,已知圆E:x2+(y-t)2=r2(t>0,r>0)经过椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,在平面直角坐标系xOy中,已知圆E:x2+(y-t)2=r2(t>0,r>0)经过椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.分析 (Ⅰ)由三角形的中位线定理,求得丨AF2丨,再由椭圆的定义,丨AF1丨=2a-丨AF2丨,根据勾股定理即可求得t的值,由EF1为半径,即可求得r的值,求得圆E的方程;
(Ⅱ)设直线l的方程为y=$\frac{\sqrt{2}}{2}x$+m,代入椭圆方程,利用韦达定理,弦长公式和基本不等式的性质,即可求得△AMN的面积的最大值.
解答 解:(Ⅰ)椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,长轴长2a=4,短轴长2b=2$\sqrt{2}$,焦距2c=2$\sqrt{2}$
因为F1,E,A三点共线,则F1A为圆E的直径,F2在圆E上,
则AF2⊥F1F2,所以OE为三角AF1F2中位线,
由E(0,t),则丨AF2丨=2t,
则丨AF1丨=2a-丨AF2丨=4-2t,
由勾股定理可知:丨AF1丨2=丨F1F2丨2+AF2丨2,即(4-2t)2=(2$\sqrt{2}$)2+(2t)2,
解得:t=$\frac{1}{2}$,
半径r=$\sqrt{丨O{F}_{1}{丨}^{2}+丨OE{丨}^{2}}$=$\frac{3}{2}$,
∴圆E的方程x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$;
(Ⅱ)由(Ⅰ)知,点A的坐标为($\sqrt{2}$,1),所以直线OA的斜率为$\frac{\sqrt{2}}{2}$,…6分
故设直线l的方程为y=$\frac{\sqrt{2}}{2}x$+m,
联立$\left\{\begin{array}{l}{y=\frac{\sqrt{2}}{2}x+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得x2+$\sqrt{2}$mx-m2-2=0.,…7分
设M(x1,y1),N(x2,y2),
所以x1+x2=-$\sqrt{2}$m,x1•x2=m2-2,
△=2m2-4m2+8>0,所以-2<m<2,…8分
又丨MN丨=$\sqrt{1+{k}^{2}}$•丨x1-x2丨,
=$\sqrt{1+\frac{1}{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{12-3{m}^{2}}$,…9分
因为点A到直线l的距离d=$\frac{\sqrt{6}丨m丨}{3}$,…10分
所以S△AMN=$\frac{1}{2}$丨MN丨•d=$\frac{1}{2}$•$\sqrt{12-3{m}^{2}}$•$\frac{\sqrt{6}丨m丨}{3}$,
=$\frac{\sqrt{2}}{2}$$\sqrt{(4-{m}^{2}){m}^{2}}$≤$\frac{\sqrt{2}}{2}$×$\frac{4-{m}^{2}+{m}^{2}}{2}$=$\sqrt{2}$,
当且仅当4-m2=m2,即m=±$\sqrt{2}$时等号成立,
∴△AMN的面积的最大值.$\sqrt{2}$
此时直线l的方程为y=$\frac{\sqrt{2}}{2}$x±$\sqrt{2}$.…12分
点评 本题考查椭圆定义的应用,考查直线与椭圆的位置关系,韦达定理,弦长公式及基本不等式的性质,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 8$\sqrt{2}$ | C. | 16 | D. | 16$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{6}}}{5}$ | B. | $\frac{{5\sqrt{6}}}{6}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4n | B. | 2n | C. | n | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.
为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图:将日均午休时玩手机不低于40分钟的学生称为“手机控”.| 非手机迷 | 手机迷 | 合计 | |
| 男 | x | x | m |
| 女 | y | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(k2≥x0) | 0.05 | 0.10 |
| k0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com