
| A. | 8 | B. | 8$\sqrt{2}$ | C. | 16 | D. | 16$\sqrt{2}$ |
分析 设l1的方程:y=k(x-1),l2的方程y=-$\frac{1}{k}$(x-1),与抛物线方程联立,利用韦达定理,结合向量的数量积公式,利用基本不等式,即可求$\overrightarrow{AG}$•$\overrightarrow{HB}$的最小值.
解答 解:抛物线C:y2=4x的焦点F(1,0),设l1的方程:y=k(x-1),l2的方程y=-$\frac{1}{k}$(x-1),
A(x1,y1),B(x2,y2),G(x3,y3),H(x4,y4),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,消去y得:k2x2-(2k2+4)x+k2=0,
∴x1+x2=2+$\frac{4}{{k}^{2}}$,x1x2=1.
由$\left\{\begin{array}{l}{y=-\frac{1}{k}(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,消去y得:x2-(4k2+2)x+1=0,
∴x3+x4=4k2+2,x3x4=1,…(9分)
∴$\overrightarrow{AG}$•$\overrightarrow{HB}$=($\overrightarrow{AF}$+$\overrightarrow{FG}$)($\overrightarrow{HF}$+$\overrightarrow{FB}$)=|$\overrightarrow{AF}$|•|$\overrightarrow{FB}$|+|$\overrightarrow{FG}$|•|$\overrightarrow{HF}$|,
=|x1+1|•|x2+1|+|x3+1|•|x4+1|
=(x1x2+x1+x2+1)+(x3x4+x3+x4+1)
=8+$\frac{4}{{k}^{2}}$+4k2≥8+2$\sqrt{\frac{4}{{k}^{2}}×4{k}^{2}}$=16.
当且仅当$\frac{4}{{k}^{2}}$=4k2,即k=±1时,$\overrightarrow{AG}$•$\overrightarrow{HB}$有最小值16,…(12分)
故选C.
点评 本题考查椭圆和抛物线的标准方程,考查直线与抛物线的位置关系,考查向量的数量积,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 种植地编号 | A1 | A2 | A3 | A4 | A5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,0,1) | (1,2,1) |
| 种植地编号 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (1,1,2) | (1,1,1) | (1,2,2) | (1,2,1) | (1,1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,-1) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
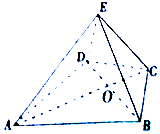 如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD,连结AC交BD于点O.
如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD,连结AC交BD于点O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
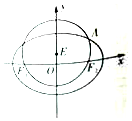 如图,在平面直角坐标系xOy中,已知圆E:x2+(y-t)2=r2(t>0,r>0)经过椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,在平面直角坐标系xOy中,已知圆E:x2+(y-t)2=r2(t>0,r>0)经过椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com