
| 种植地编号 | A1 | A2 | A3 | A4 | A5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,0,1) | (1,2,1) |
| 种植地编号 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (1,1,2) | (1,1,1) | (1,2,2) | (1,2,1) | (1,1,1) |
分析 (Ⅰ)由表可知:空气湿度指标为1的有A2,A4,A5,A7,A9,A10,空气湿度指标为2的有A1,A3,A6,A8,求出这10块种植地中任取两块地,基本事件总数n,这两块地的空气温度的指标z相同包含的基本事件个数,然后求解概率.
(Ⅱ)随机变量X=A-B的所有可能取值为1,2,3,4,5,求出概率得到分布列,然后求解期望即可.
解答 解:(Ⅰ)由表可知:空气湿度指标为1的有A2,A4,A5,A7,A9,A10…(1分)
空气湿度指标为2的有A1,A3,A6,A8,…(2分)
在这10块种植地中任取两块地,基本事件总数n=$C_{10}^2=\frac{10×9}{2}=45$…(3分)
这两块地的空气温度的指标z相同包含的基本事件个数$m=C_6^2+C_4^2=\frac{6×5}{2}+\frac{4×3}{2}=21$…(5分)
∴这两地的空气温度的指标z相同的概率$P=\frac{m}{n}=\frac{21}{45}=\frac{7}{15}$…(6分)
(Ⅱ)由题意得10块种植地的综合指标如下表:
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 综合指标 | 4 | 4 | 6 | 1 | 4 | 4 | 3 | 5 | 4 | 3 |
| X | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{10}{21}$ | $\frac{2}{21}$ | $\frac{7}{21}$ | $\frac{1}{21}$ | $\frac{1}{21}$ |
点评 本题考查离散性随机变量的分布列的求法,概率的求法,考查转化思想以及计算能力.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
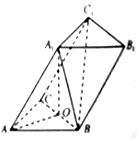 如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.
如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 8$\sqrt{2}$ | C. | 16 | D. | 16$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com