
分析 (1)由已知递推式a2-a1=2p-q,a3-a2=4p-2q,a4-a3=8p-3q,再由等差数列的定义列等式求得p=q=0;
(2)q=0,则${a}_{n+1}={a}_{n}+p•{2}^{n}$,由等比数列的性质列式求得p=0或p=$\frac{1}{2}$.然后分类求得数列{an}的通项公式;
(3)p=1时,${a}_{n}-{a}_{5}={2}^{n}-32-\frac{(n+4)(n-5)}{2}q$,可得当n≥6时,an-a5≥0恒成立,利用作差法求得满足条件的q的最大值;当n≤4时,需满足an-a5≤0恒成立,对n=1、2、3、4验证求得q的最小值,从而可得q的取值范围.
解答 解:(1)由已知递推式可得,a1=1,a2=1+2p-q;
a2-a1=2p-q,a3-a2=4p-2q,a4-a3=8p-3q.
由等差数列知,a4-a3=a3-a2=a2-a1,得p=q=0;
(2)q=0,则${a}_{n+1}={a}_{n}+p•{2}^{n}$,
由${a}_{1}{a}_{3}={{a}_{2}}^{2}$,得p=0或p=$\frac{1}{2}$.
当p=0时,an+1=an,an=1,满足题意;
当p=$\frac{1}{2}$时,由累加法得${a}_{n}={2}^{n-1}$,满足题意;
(3)p=1时,${a}_{n}-{a}_{5}={2}^{n}-32-\frac{(n+4)(n-5)}{2}q$,
当n≥6时,由an-a5≥0恒成立得,q≤$\frac{{2}^{n+1}-64}{(n+4)(n-5)}$恒成立.
设${c}_{n}=\frac{{2}^{n+1}-64}{(n+4)(n-5)}$,只需求出cn的最小值.
${c}_{n+1}-{c}_{n}=\frac{{2}^{n+1}({n}^{2}-3n-20)+128n}{(n+4)(n+5)(n-4)(n-5)}$.
当n≥7时,n2-3n-20=n(n-3)-20≥8>0,有cn+1>cn;
当n=6时,直接验证c7>c6;
故c6为最小值,其值为$\frac{32}{5}$,∴q$≤\frac{32}{5}$;
当n≤4时,需满足an-a5≥0恒成立,
对n=1、2、3、4验证,
n=1,q≥3;n=2,q$≥\frac{28}{9}$;n=3,q$≥\frac{24}{7}$;n=4,q≥4.
综上,4$≤q≤\frac{32}{5}$.
点评 本题考查数列递推式,考查等比关系的确定,训练了作差法比较两个函数值的大小,考查逻辑思维能力与推理运算能力,属难题.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
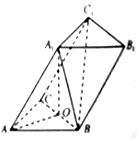 如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.
如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
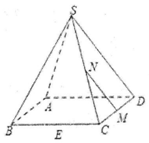 如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 8$\sqrt{2}$ | C. | 16 | D. | 16$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com