
五个人站成一排,求在下列条件下的不同排法种数:
(1)甲必须在排头;
(2)甲、乙相邻;
(3)甲不在排头,并且乙不在排尾;
(4)其中甲、乙两人自左向右从高到矮排列且互不相邻.
(1)24;(2)48;(3)78;(4)36
解析试题分析:(1)特殊元素(位置)法:首先排“排头”不动,再排其它4个位置有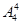 种共有24种;(2)捆绑法:把甲、乙看成一个人来排有
种共有24种;(2)捆绑法:把甲、乙看成一个人来排有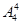 种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为
种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为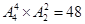 种;(3)对立法:甲在排头和乙在排尾的各
种;(3)对立法:甲在排头和乙在排尾的各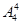 种,其中甲在排头且乙在排尾的有
种,其中甲在排头且乙在排尾的有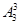 种,五个人站成一排的不同排法数是
种,五个人站成一排的不同排法数是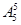 种,所以甲不在排头,并且乙不在排尾的有
种,所以甲不在排头,并且乙不在排尾的有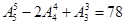 种;(4)插空法:先将其余3个全排列
种;(4)插空法:先将其余3个全排列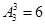 种,再将甲、乙插入4个空位
种,再将甲、乙插入4个空位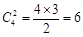 种, 所以,一共有
种, 所以,一共有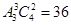 种不同排法.
种不同排法.
试题解析:(1)特殊元素是甲,特殊位置是排头;首先排“排头”不动,再排其它4个位置有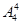 种,所以共有:
种,所以共有: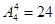 种
种
把甲、乙看成一个人来排有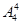 种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为
种,而甲、乙也存在顺序变化,所以甲、乙相邻排法种数为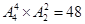 种;
种;
(3)甲不在排头,并且乙不在排尾排法种数为: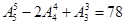 种;先将其余3个全排列
种;先将其余3个全排列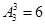 ,再将甲、乙插入4个空位
,再将甲、乙插入4个空位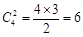 ,所以,一共有
,所以,一共有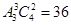 种不同排法.
种不同排法.
考点:排列组合


科目:高中数学 来源: 题型:解答题
有9本不同的课外书,分给甲、乙、丙三名同学,求在下列条件下,各有多少种分法?
(1)甲得4本,乙得3本,丙得2本;
(2)一人得4本,一人得3本,一人得2本;
(3)甲、乙、丙各得3本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com