
已知数列{an}是首项为a且公比q不等于1的等比数列,Sn是其前n项和,a1,2a7,3a4成等差数列.
(Ⅰ) 证明12S3,S6,S12-S6成等比数列;
(Ⅱ)求和Tn=a1+2a4+3a7+…+na3n-2.
(Ⅰ)证明:由a1,2a7,3a4成等差数列.得4a7=a1+3a4,即4aq6=a+3aq3.变形得(4q3+1)(q3-1)=0,所以q3=- 或q3=1(舍去)由
或q3=1(舍去)由
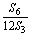 =
=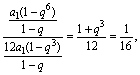
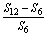 =
=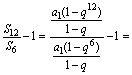 1+q6-1=q6=
1+q6-1=q6=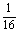 ,
,
得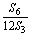 =
=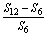 .所以12S3,S6,S12-S6成
.所以12S3,S6,S12-S6成 等比数列.
等比数列.
(Ⅱ)解法
:Tn=a1+2a4+3a7+…+na3a-2=a+2aq3+3aq6+…+naq3(n-2),
即Tn=a+2·(- )a+3·(-
)a+3·(- )2a+…+n·(-
)2a+…+n·(- )n-1a. ①
)n-1a. ①
①×(- )3a得:-
)3a得:- Tn=-
Tn=- a+2·(-
a+2·(- )2a+3·(-
)2a+3·(- )3a+…+n·(-
)3a+…+n·(- )na ②
)na ②
①-②有: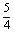 Tn=a+(-
Tn=a+(- )a+(-
)a+(- )2a+(-
)2a+(- )3a+…(-
)3a+…(- )n-1a-n·(-
)n-1a-n·(- )na=
)na=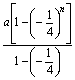 -n·(-
-n·(- )na=
)na=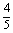 a-(
a-(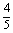 +n)·(-
+n)·(- )na.所以Tn=
)na.所以Tn=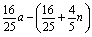 ·(-
·(- )na.
)na.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
若函数f(x)=loga(2x2+x)(a>0且a≠1)在区间(0, 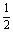 )内恒有f(x)>0,则f(x)的单调递增区间为 ( )
)内恒有f(x)>0,则f(x)的单调递增区间为 ( )
A.(-∞,-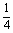 ) B.(-
) B.(-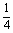 ,+∞) C.(0,+∞) D.(-∞,-
,+∞) C.(0,+∞) D.(-∞,-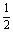 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=x2+2bx+c(c<b<1),f(1)=0.且方程f(x)+1=0有实根.
(1)证明:-3<c≤-1且b≥0.
(2)若m是方程f(x)+1=0的一个实根,判断f(m-4)的正负并加以说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
设无穷等差数列{an}的前n项和为Sn.
(Ⅰ)若首项a1=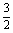 ,公差d=1,求满足Sk2=(Sk)2的正整数k;
,公差d=1,求满足Sk2=(Sk)2的正整数k;
(Ⅱ)求所有的无穷等差数列{an};使得对于一切正整数中k都有Sk2=(Sk)2成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
假设某市:2004年新建住房400万平方米,其中有250万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,
(1)该市历年所建中低价房的累计面积(以2004年为累计的第一年)将首次不少于4750万平方米?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?
(3)设几年后新建住房面积S为:400(1+8%)n. 85%<25n2+225n.
查看答案和解析>>
科目:高中数学 来源: 题型:
若数列{an}是等比数列,则数列{an+an+1} ( )
A.一定是等比数列
B.可能是等比数列,也可能是等差数列
C.一定是等差数列
D.一定不是等比数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com