
【题目】如图,在菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF//AE,AB=AE=2.
(1)求证:BD⊥平面ACFE;
(2)当直线FO与平面BDE所成的角为45°时,求二面角B﹣EF﹣D的余弦值.
【答案】
(1)证明:在菱形 ![]() 中,可得
中,可得 ![]() ,又因为
,又因为 ![]() 平面
平面 ![]() ,
, ![]() ,且
,且 ![]() 平面
平面 ![]()
(2)解:取 ![]() 的中点为
的中点为 ![]() ,以
,以 ![]() 为坐标原点,以
为坐标原点,以 ![]() 为
为 ![]() 轴,以
轴,以 ![]() 为
为 ![]() 轴,以
轴,以 ![]() 为
为 ![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则 ![]() ,则
,则 ![]() ,设平面
,设平面 ![]() 的法向量
的法向量 ![]() ,
,
由  ,也就是
,也就是 ![]() ,可取
,可取 ![]() ①
①
则 ![]() ,解得
,解得 ![]() ,故
,故 ![]()
![]()
设平面 ![]() 的法向量为
的法向量为 ![]()
设平面 ![]() 的法向量为
的法向量为 ![]() ,
,
同理①可得 ![]()
则 ![]() ,则二面角
,则二面角 ![]() 的余弦值为
的余弦值为 ![]()
【解析】本题主要考查空间二面角的求法以及线面垂直的判定定理的应用。(1)主要是利用线面垂直的判定定理和性质定理进行证明。(2)建立空间直角坐标系,利用向量坐标进行求解。
【考点精析】关于本题考查的直线与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.存在 ![]() ,使得
,使得 ![]() 的否定是:不存在
的否定是:不存在 ![]() ,使得
,使得 ![]()
B.对任意 ![]() ,均有
,均有 ![]() 的否定是:存在
的否定是:存在 ![]() ,使得
,使得 ![]()
C.若 ![]() ,则
,则 ![]() 或
或 ![]() 的否命题是:若
的否命题是:若 ![]() ,则
,则 ![]() 或
或 ![]()
D.若 ![]() 为假命题,则命题
为假命题,则命题 ![]() 与
与 ![]() 必一真一假
必一真一假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为
的最小正周期为 ![]() ,将函数
,将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位长度,再向下平移
个单位长度,再向下平移 ![]() 个单位长度,得到函数
个单位长度,得到函数 ![]() 的图象.
的图象.
(Ⅰ)求函数 ![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)在锐角 ![]() 中,角
中,角 ![]() 的对边分别为
的对边分别为 ![]() .若
.若 ![]() ,
, ![]() ,求
,求 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形 ![]() 中,点
中,点 ![]() 在线段
在线段 ![]() 上,
上, ![]() ,
, ![]() ,沿直线
,沿直线 ![]() 将
将 ![]() 翻折成
翻折成 ![]() ,使点
,使点 ![]() 在平面
在平面 ![]() 上的射影
上的射影 ![]() 落在直线
落在直线 ![]() 上.
上.
(Ⅰ)求证:直线 ![]() 平面
平面 ![]() ;
;
(Ⅱ)求二面角 ![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.8元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照 ![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
(ⅰ)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费 ![]() (元)与月份
(元)与月份 ![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是 ![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图程序框图是为了求出满足3n﹣2n>1000的最小偶数n,那么在 ![]() 和
和 ![]() 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )
A.A>1000和n=n+1
B.A>1000和n=n+2
C.A≤1000和n=n+1
D.A≤1000和n=n+2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义域为R的周期函数,最小正周期为2,且f(1+x)=f(1-x),当-1≤x≤0时,f(x)=-x.
(1)判断f(x)的奇偶性;
(2)试求出函数f(x)在区间[-1,2]上的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018福建福州市一中高三上学期期中考试】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,点
,点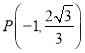 在椭圆上,且
在椭圆上,且![]() 与
与![]() 轴交点恰为
轴交点恰为![]() 中点.
中点.
(I)求椭圆![]() 的方程;
的方程;
(II)过![]() 作两条互相垂直的直线,分别交椭圆
作两条互相垂直的直线,分别交椭圆![]() 于点
于点![]() 和
和![]() .求四边形
.求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com