
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
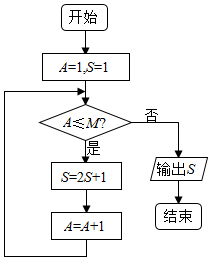
分析 由图知,每次进入循环体后,S的值被施加的运算是乘以2加上1,由此运算规律进行计算,经过运算后输出的结果是63,从而得解.
解答 解:由图知运算规则是对S=2S+1,执行程序框图,可得
A=1,S=1
满足条件A≤M,第一次进入循环体后S=2×1+1=3,
满足条件A≤M,第二次进入循环体后S=2×3+1=7,
满足条件A≤M,第三次进入循环体后S=2×7+1=15,
满足条件A≤M,第四次进入循环体后S=2×15+1=31,
满足条件A≤M,第五次进入循环体后S=2×31+1=63,
由于A的初值为1,每进入一次循环体其值增大1,第五次进入循环体后A=5.
故判断框中的整数M的值应为5,这样就可保证循环体只能被运行五次.
故选:A.
点评 本题考查循环结构,已知运算规则与最后运算结果,求运算次数的一个题.是算法中一种常见的题型,属于基础题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
| A. | $[\frac{{3\sqrt{5}}}{2},+∞)$ | B. | $(1,\frac{3}{2}]$ | C. | $(1,\frac{{3\sqrt{5}}}{2}]$ | D. | $[\frac{3}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
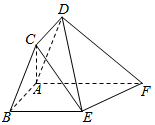 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e3+1 | B. | e3+2 | C. | e3+e+1 | D. | e3+e+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
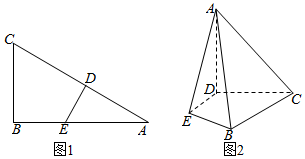 已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).
已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a6 | B. | a8 | C. | a9 | D. | a10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com