
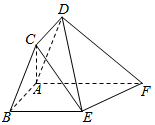
 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.分析 (1)证明AC⊥AB,利用平面ABCD⊥平面ABEF,根据面面垂直的性质定理即可证明AC⊥平面ABEF;
(2)由(1)可知,AC是三棱锥D-AEF的高,利用体积公式求三棱锥D-AEF的体积.
解答 (1)证明:∵AB=1,BC=2,∠CBA=$\frac{π}{3}$,
∴AC2=AB2+BC2-2AB•BCcos$\frac{π}{3}$=1+4-2×2×1×$\frac{1}{2}$=3,
则AC=$\sqrt{3}$,满足BC2=AB2+AC2,
即△CAB是直角三角形,AC⊥AB,
∵平面ABCD⊥平面ABEF,AC?平面ABCD,平面ABCD∩平面ABEF=AB,
∴AC⊥平面ABEF;
(2)解:由(1)可知,AC是三棱锥D-AEF的高,
∵S△AEF=$\frac{1}{2}×3×1$=$\frac{3}{2}$,
∴三棱锥D-AEF的体积V=$\frac{1}{3}×\frac{3}{2}×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题主要考查面面垂直的性质定理,线面垂直的证明,考查三棱锥D-AEF的体积,正确运用面面垂直的性质定理是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
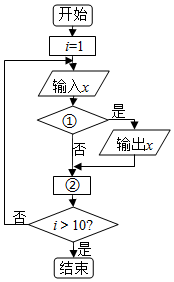 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )| A. | x>60?,i=i+1 | B. | x<60?,i=i+1 | C. | x>60?,i=i-1 | D. | x<60?,i=i-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{4-2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com