
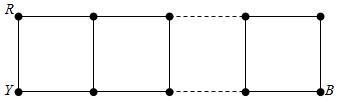
分析 需要分类讨论,记P=R(或Y),Q=B时的着色数目为an,记P=B,Q=R(或Y)时的着色数目为bn,记P=R,Q=Y或者P=Y,Q=R时的着色数目为cn,根据端点的个数不同,分别求出找到相应的规律,即可得到an=2bn-1+cn-1=an-1+bn-1+cn-1=3n-2,问题得以解决.
解答 解:2×n格点链中的2n个结点用红(R)、黄(Y)、蓝(B)三种颜色染色,其中最左端点染成红色与黄色,设右端点染色为P,Q,如图所示: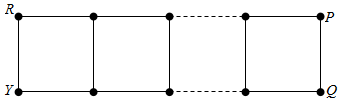
记P=R(或Y),Q=B时的着色数目为an,
记P=B,Q=R(或Y)时的着色数目为bn,
记P=R,Q=Y或者P=Y,Q=R时的着色数目为cn,
我们注意到:(1)若右端没有约束时,每增加一个格子都有3种不同的着色方法,则an+bn+cn=3n-1,
(2)由对称性,即将图形山下翻转,并且颜色R与Y互换,可知an=bn,
(3)考虑相互的递推特征,如图:则an=2bn-1+cn-1,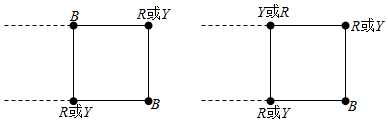
所以,$\left\{\begin{array}{l}{{a}_{n}+{b}_{n}+{c}_{n}={3}^{n-1}}\\{{a}_{n}={b}_{n}}\\{{a}_{n}=2{b}_{n-1}+{c}_{n-1}}\end{array}\right.,n∈N*$
这样an=2bn-1+cn-1=an-1+bn-1+cn-1=3n-2,
即为问题所求的不同的染色方法数.
点评 本题考查了着色问题,关键是需要分类讨论,以及找到相应的规律,属于难题.


科目:高中数学 来源: 题型:解答题
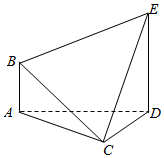 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AB=CD=1,AC=$\sqrt{3}$,AD=DE=2.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AB=CD=1,AC=$\sqrt{3}$,AD=DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,2) | C. | (1,1+$\sqrt{2}$) | D. | (2,2+$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
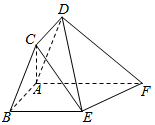 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
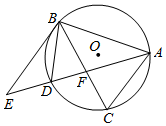 如图,△ABC内接于圆O,过B点的切线为BE,∠CBE的角平分线交圆O于点D,连接AD交BC于F,延长交BE于E.
如图,△ABC内接于圆O,过B点的切线为BE,∠CBE的角平分线交圆O于点D,连接AD交BC于F,延长交BE于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com