
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 由新定义知,重点在于确定函数f(x)=x2在[-1,t]上的最值,故讨论以确定函数的最值,再由最值确定各段上的最小值k,从而确定k的值.
解答 解:①当-1<t<0时,
f(x)=x2在[-1,t]上的最小值N(t)=t2,最大值M(t)=1,
故M(t)-N(t)=1-t2=(1-t)(1+t)≤2(1+t);
②当0≤t≤1时,
f(x)=x2在[-1,t]上的最小值N(t)=0,最大值M(t)=1,
故M(t)-N(t)=1≤1+t;
③当1<t≤4时,
f(x)=x2在[-1,t]上的最小值N(t)=0,最大值M(t)=t2,
故M(t)-N(t)=t2≤4(1+t);
综上所述,
k=4;
故选A.
点评 本题考查了学生对新定义的接受与转化能力及分类讨论的思想应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
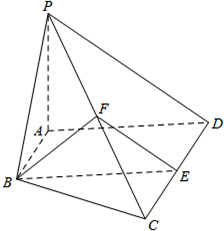 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AD=CD=2AB=2PA=4,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AD=CD=2AB=2PA=4,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 工序时间原料 | 粗加工 | 精加工 |
| 原料A | 9 | 15 |
| 原料B | 6 | 21 |
| A. | 36 | B. | 42 | C. | 45 | D. | 51 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com