
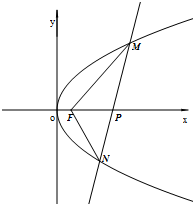
 已知曲线C上任意一点到点F(1,0)的距离比到直线x+2=0的距离小1,点P(4,0).
已知曲线C上任意一点到点F(1,0)的距离比到直线x+2=0的距离小1,点P(4,0).分析 (Ⅰ)由题意可得,点P到F(1,0)的距离与到直线x=-1的距离相等,由抛物线的定义可得点的轨迹是以F(1,0)为焦点,以x=-1为准线的抛物线,从而可求曲线C的方程;
(Ⅱ)设Q(x,y),再由两点的距离公式,结合抛物线方程,配方即可得到所求最小值;
(Ⅲ)方法一、设直线l:x=my+4,M(x1,y1),N(x2,y2),联立抛物线方程,运用韦达定理和弦长公式、三角形面积公式计算即可得到;
方法二、讨论直线的斜率不存在,不成立;设直线l:y=k(x-4),(k≠0),M(x1,y1),N(x2,y2),联立抛物线方程,运用韦达定理和弦长公式、三角形面积公式计算即可得到直线方程.
解答 解:(I)由题意,P到F(1,0)距离等于它到直线x=-1的距离,
由抛物线定义,知C为抛物线,F(1,0)为焦点,x=-1为准线,
所以C的方程为y2=4x; …3分
(II)解:设Q(x,y),
则$|PQ|=\sqrt{{{(x-4)}^2}+{y^2}}=\sqrt{{{(x-4)}^2}+4x}$=$\sqrt{{{(x-2)}^2}+12}$
∴$当x=2时,|PQ{|_{min}}=2\sqrt{3}$…3分
(Ⅲ)解:设直线l:x=my+4,M(x1,y1),N(x2,y2),
焦点F(1,0)
由$\left\{\begin{array}{l}x=my+4\\{y^2}=4x\end{array}\right.$消去x得y2-4my-16=0,
由韦达定理可得$\left\{\begin{array}{l}{y_1}+{y_2}=4{m_{\;}}\\{y_1}{y_2}=-16\end{array}\right.$,
所以△FMN的面积${S_{△FMN}}=\frac{1}{2}|PF|•|{y_1}-{y_2}|$=$\frac{1}{2}•3•\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}$
=$\frac{3}{2}•\sqrt{{{(4m)}^2}+64}=6\sqrt{{m^2}+4}=6\sqrt{5}$,
∴m=±1,
所以直线l的方程为:x±y-4=0…12分
(方法二)解:若直线l的斜率不存在,则l:x=4,M(4,4),N(4,-4)
所以△FMN的面积${S_{△FMN}}=\frac{1}{2}|CF|•8$=$\frac{1}{2}•3•8=12≠6\sqrt{5}$,不符合
所以直线l的斜率必存在
设直线l:y=k(x-4),(k≠0),M(x1,y1),N(x2,y2),焦点F(1,0)
由$\left\{\begin{array}{l}y=k(x-4)\\{y^2}=4x\end{array}\right.$消去y得k2x2-4(2k2+1)x+16k2=0
由韦达定理可得$\left\{\begin{array}{l}{x_1}+{x_2}=\frac{{4(2{k^2}+1)}}{k^2}\\{x_1}{x_2}=16\end{array}\right.$
弦长$|MN|=\sqrt{(1+{k^2})[{{({x_1}+{x_2})}^2}-4{x_1}{x_2}]}$=$\sqrt{(1+{k^2})[{{(8+\frac{4}{k^2})}^2}-64]}$=$\sqrt{\frac{{16(1+{k^2})(1+4{k^2})}}{k^4}}$,
F到l的距离$d=\frac{|3k|}{{\sqrt{1+{k^2}}}}$.
所以△FMN的面积${S_{△FMN}}=\frac{1}{2}|MN|•d$=$6\sqrt{\frac{{1+4{k^2}}}{k^2}}=6\sqrt{5}$
∴k=±1
所以直线l的方程为:x±y-4=0…12分.
点评 本题考查抛物线的定义、方程和性质,主要考查抛物线方程和直线方程联立,运用韦达定理和弦长公式、三角形面积公式,考查运算化简能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (e,4) | B. | $(\frac{1}{{\sqrt{e}}},+∞)$ | C. | (0,e) | D. | $(0,\frac{1}{{\sqrt{e}}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 2 | 3 | 5 | 11 | 8 | 7 | 9 | 3 | 10 |
| A. | 10741 | B. | 10736 | C. | 10731 | D. | 10726 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{10}$ | B. | $\sqrt{10}$ | C. | $\sqrt{13}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com