
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 2 | 3 | 5 | 11 | 8 | 7 | 9 | 3 | 10 |
| A. | 10741 | B. | 10736 | C. | 10731 | D. | 10726 |
分析 由题意知数列{xn}满足x1=2,xn+1=f(xn),从而得到数列从第二项起是周期数列,周期为3,一个周期内的和为16,由此能求出x1+x2+x3+x4+…+x2015的值.
解答 解:由题意知:
数列{xn}满足x1=2,且对任意n∈N*,
点(xn,xn+1)都在函数y=f(x)的图象上,
∴xn+1=f(xn)
∴x1=2,x2=3,x3=5,x4=8,x5=3,x6=5,x7=8,x8=3…
所以数列从第二项起是周期数列,周期为3,一个周期内的和为16,
所以x1+x2+x3+x4+…+x2015=2+671×(x1+x2+x3)+x2=10741.
故选:A.
点评 本题考查数列前2015项和的求法,是中档题,解题时要认真审题,注意数列的周期性的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x2+4x+4(x≥-2) | B. | y=x2-4x+4(x≥0) | C. | y=x2+2(x≥0) | D. | y=x2-2(x≥0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既不是奇函数又不是偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
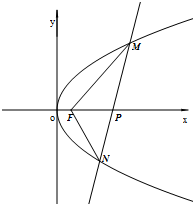 已知曲线C上任意一点到点F(1,0)的距离比到直线x+2=0的距离小1,点P(4,0).
已知曲线C上任意一点到点F(1,0)的距离比到直线x+2=0的距离小1,点P(4,0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com