
已知椭圆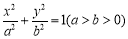 的离心率
的离心率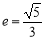 ,且直线
,且直线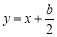 是抛物线
是抛物线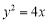 的一条切线.
的一条切线.
(1)求椭圆的方程;
(2)点P 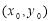 为椭圆上一点,直线
为椭圆上一点,直线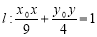 ,判断l与椭圆的位置关系并给出理由;
,判断l与椭圆的位置关系并给出理由;
(3)过椭圆上一点P作椭圆的切线交直线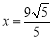 于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
(1) 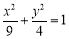 ;(2) 直线l与椭圆相切;(3)
;(2) 直线l与椭圆相切;(3)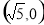
【解析】
试题分析:(1)直线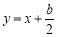 是抛物线
是抛物线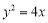 的一条切线.所以将直线代入抛物线方程,即
的一条切线.所以将直线代入抛物线方程,即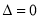 ,得出
,得出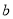 的值,利用
的值,利用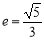 ,椭圆中
,椭圆中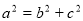 ,依次解出
,依次解出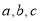 ,从而解出方程;
,从而解出方程;
(2)直线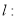
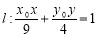 与椭圆方程联立,注意用到平方相减消
与椭圆方程联立,注意用到平方相减消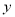 ,得到关于
,得到关于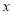 的方程,求其
的方程,求其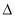 ,利用点
,利用点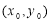 在椭圆上的条件,判定直线与椭圆的位置关系;
在椭圆上的条件,判定直线与椭圆的位置关系;
(3)首先取两种特殊情形:切点分别在短轴两端点时,求其切线方程,并求他们的交点,交点有可能是恒过的定点,如果是圆上恒过的定点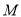 ,如果是则需满足,
,如果是则需满足,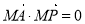 ,从而判定所求交点是否是真正的定点.此题属于较难习题.
,从而判定所求交点是否是真正的定点.此题属于较难习题.
试题解析:(1)因为直线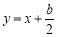 是抛物线
是抛物线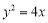 的一条切线,所以
的一条切线,所以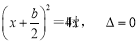 ,
,
即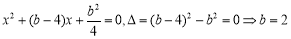 2分
2分
又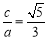 ,所以
,所以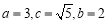 ,
,
所以椭圆的方程是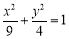 . 4分
. 4分
(2)由 得
得
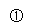
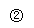 由①2+②
由①2+②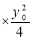 得
得
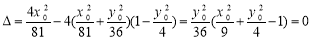
∴直线l与椭圆相切 9分
(3)首先取两种特殊情形:切点分别在短轴两端点时,
求得两圆的方程为
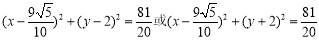 ,
,
两圆相交于点(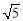 ,0),(
,0),(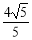 ,0),
,0),
若定点为椭圆的右焦点(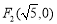 .
.
则需证: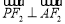 .
.
设点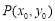 ,则椭圆过点P的切线方程是
,则椭圆过点P的切线方程是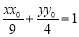 ,
,
所以点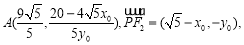
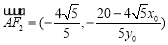 ,
,
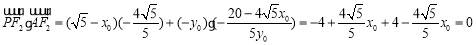 所以
所以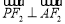 . 11分
. 11分
若定点为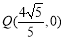 ,
,
则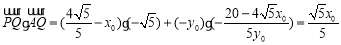 ,不满足题意.
,不满足题意.
综上,以线段AP为直径的圆恒过定点(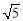 ,0). 14分
,0). 14分
考点:1.椭圆的性质与方程;2.直线与圆锥曲线相交时的综合问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年湖北省宜昌示范教学协作体高一下学期期中考试数学试卷(解析版) 题型:选择题
已知等比数列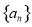 的公比为2,前4项的和是1,则前8项的和为( )
的公比为2,前4项的和是1,则前8项的和为( )
A.23 B.21 C.19 D.17
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:填空题
已知 展开式各项的系数和比各项的二次式系数和大992,则展开式中系数最大的项是第 项.
展开式各项的系数和比各项的二次式系数和大992,则展开式中系数最大的项是第 项.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:选择题
设 在(
在( )上单调递增;
)上单调递增; ,则p是q的( )
,则p是q的( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷(解析版) 题型:填空题
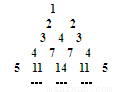
观察如图三角形数阵,则
(1)若记第n行的第m个数为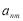 ,则
,则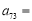 .
.
(2)第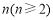 行的第2个数是 .
行的第2个数是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷(解析版) 题型:选择题
已知函数 是定义在R上的可导函数,其导函数记为
是定义在R上的可导函数,其导函数记为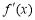 ,若对于任意实数x,有
,若对于任意实数x,有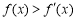 ,且
,且 为奇函数,则不等式
为奇函数,则不等式 的解集为( )
的解集为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:填空题
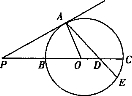
如图,已知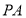 是⊙
是⊙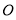 的切线,
的切线,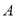 是切点,直线
是切点,直线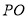 交⊙
交⊙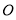 于
于 两点,
两点,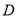 是
是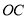 的中点,连接
的中点,连接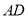 并延长交⊙
并延长交⊙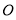 于点
于点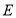 ,若
,若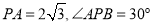 ,则
,则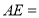 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(二)理科数学试卷(解析版) 题型:解答题
设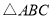 的三内角
的三内角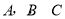 所对的边长分别为
所对的边长分别为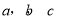 ,且
,且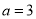 ,A=
,A= ,
,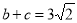 .
.
(1)求三角形ABC的面积;
(2)求 的值及
的值及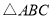 中内角B,C的大小.
中内角B,C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com