练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．3名学生报名参加艺术体操、美术、计算机、航模四个课外兴趣小组，每人选报一种，则不同的报名种数有64．

    分析 根据题意，易得3名同学中每人有4种报名方法，由分步计数原理计算可得答案．

    解答 解：根据题意，每个学生可以在艺术体操、美术、计算机、航模课外兴趣小组中任选1个，有4种选法，
    则3名学生一共有4×4×4=43=64种不同的报名情况；
    故答案为：64．

    点评 本题考查分步计数原理的运用，解题时注意题干条件中“每人选报一种”的限制条件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．在△ABC中，$\overrightarrow{AB}⊥\overrightarrow{AC}$，$\overrightarrow{AB}=（1，-2）$，$\overrightarrow{AC}=（4，λ）$，则λ=（　　）
    A．-2B．2C．8D．-8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

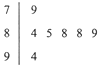    1．如图是2015年日喀则市举办青少年运动会上，7位裁判为某武术队员打出的分数的茎叶图，左边数字表示十位数字，右边数字表示个位数字．这些数据的中位数是______，去掉一个最低分和最高分后所剩数据的平均数是（　　）
    A．86.5； 86.7B．88； 86.7C．88；86.8D．86.5；86.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若$\frac{2+ai}{1+i}$=x+yi（a，x，y∈R），且xy＞1，则实数a的取值范围是（　　）
    A．（2$\sqrt{2}$，+∞）B．（-∞，-2$\sqrt{2}$）∪（2$\sqrt{2}$，+∞）C．（-2$\sqrt{2}$，2）∪（2$\sqrt{2}$，+∞）D．（-∞，-2）∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．函数f（x）=lnx-2x的单调递增区间为（　　）
    A．（-∞，2）B．$（-∞，\frac{1}{2}）$C．$（0，\frac{1}{2}）$D．$（\frac{1}{2}，+∞）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．设函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}x，0＜x≤9}\\{f（x-4），x＞9}\end{array}\right.$，则f（13）的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=loga（3-ax）．
    （1）当x∈[0，2]时，函数f（x）恒有意义，求实数a的取值范围．
    （2）若函数f（x）在区间[1，2]上为减函数，且最大值为2，求出实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若复数z的共轭复数$\overline z$满足$\overline z•i=3+4i$，则复数z的虚部是3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．平面直角坐标系中，已知O为坐标原点，点A、B的坐标分别为（1，1）、（-3，3）．若动点P满足$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$，其中λ、μ∈R，且λ+μ=1，则点P的轨迹方程为（　　）
    A．x-y=0B．x+y=0C．x+2y-3=0D．（x+1）2+（y-2）2=5

    查看答案和解析>>

    同步练习册答案