
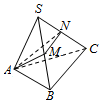
 如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值.
如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值. 分析 将三棱锥S-ABC侧面沿侧棱SA剪开,将3个侧面铺平展开,成曲边扇形S-ABCA',由此能求出△AMN的周长的最小值.
解答 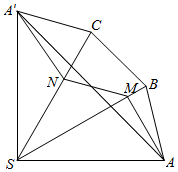 解:∵一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,
解:∵一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,
M、N分别为棱SB和SC上的点,
将三棱锥S-ABC侧面沿侧棱SA剪开,
将3个侧面铺平展开,成曲边扇形S-ABCA',
∵SA=SB=SC=1,∠ASB=30°,
∴∠ASA'=90°,
△AMN的边展成了折线AMNA',连接AA',
∵平面内两点之间线段最短,
∴三角形AMN周长AM+MN+NA'≥AA'=$\sqrt{2}$,
∴三角形AMN的周长的最小值为$\sqrt{2}$.
点评 本题考查三角形的周长的最小值的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
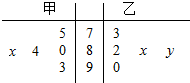 在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )
在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
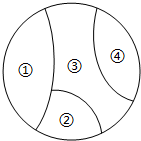 将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )
将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com