
分析 根据题意分别令x取“x+m”、“x+2m”代入式子化简,由周期的定义可求出函数的最小正周期.
解答 解:因为对x∈R,有f(x+m)=$\frac{1+f(x)}{1-f(x)}$恒成立,
所以f(x+2m)=$\frac{1+f(x+m)}{1-f(x+m)}$=$\frac{1+\frac{1+f(x)}{1-f(x)}}{1-\frac{1+f(x)}{1-f(x)}}$=-$\frac{1}{f(x)}$,
则f(x+4m)=-$\frac{1}{f(x+2m)}$=-$\frac{1}{-\frac{1}{f(x)}}$=f(x),
则f(x)的周期是4m,
故答案为:4m.
点评 本题考查函数周期的定义,以及赋值法的应用,考查化简、变形能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a⊥α,b⊥α,则a⊥b | B. | a∥α,b?α,则a∥b | ||
| C. | a⊥b,b?α,则a⊥α | D. | a∥α,b?α,a?α,则a∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
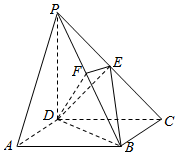 如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
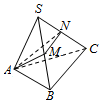 如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值.
如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com