
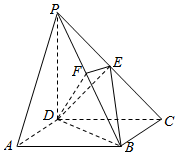
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.分析 (1)连结AC,设AC交BD于O,连结EO,则PA∥EO,由此能证明PA∥平面EO.
(2)由已知得PD⊥BC,CD⊥BC,从而BC⊥平面PDC,进而BC⊥DE,再由DE⊥PC,DE⊥PB,由此能证明PB⊥平面DEF.
解答 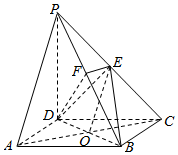 证明:(1)连结AC,设AC交BD于O,连结EO,
证明:(1)连结AC,设AC交BD于O,连结EO,
∵底面ABCD中矩形,∴点O是AC的中点,
又∵点E是PC的中点,∴PA∥EO,
∵EO?平面BDE,PA?平面BDE,
∴PA∥平面EO.
(2)PD⊥底面ABCD,BC?底面ABCD,
∴PD⊥BC,
∵底面ABCD中矩形,∴CD⊥BC,
∵PD∩CD=D,∴BC⊥平面PDC,
∵DE?平面PDC,∴BC⊥DE,
∵PD=DC,E是PC的中点,∴DE⊥PC,
∵PC∩BC=C,∴DE⊥PB,
又∵EF⊥PB,DE∩EF=E,DE?平面DEF,EF?平面DEF,
∴PB⊥平面DEF.
点评 本查线面平行的证明,考查线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
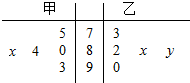 在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )
在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com