
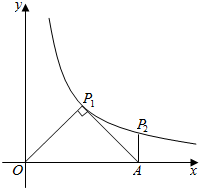
分析 设P2的坐标为(a,1),根据条件得到P1($\frac{1}{2}a$,$\frac{1}{2}$a),代入双曲线y=$\frac{k}{x}$,解方程即可得到结论.
解答 解:∵AP2⊥x轴且AP2=1,
∴设P2(a,1),则|OA|=a,(a>0)
∵,△AOP1为等腰直角三角形,
∴P1($\frac{1}{2}a$,$\frac{1}{2}$a),
∵曲线y=$\frac{k}{x}$经过P1,P2两点,
则$\left\{\begin{array}{l}{\frac{k}{a}=1}\\{\frac{1}{2}a=\frac{k}{\frac{1}{2}a}}\end{array}\right.$,即$\left\{\begin{array}{l}{a=k}\\{\frac{1}{4}{a}^{2}=k}\end{array}\right.$,得a=k=4.
点评 本题主要考查双曲线的图象和性质,根据条件求出点的坐标,建立方程关系是解决本题的关键.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
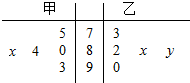 在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )
在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
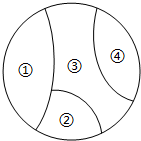 将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )
将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com