
分析 先求出$f′(x)=x+\frac{a}{x}$,分别讨论a>0和a<0时的情况,从而求出单调区间.
解答 f′(x)=$x+\frac{a}{x}$,
①当a>0时,f′(x)>0,则f(x)在(0,+∞)上单调递增;
②当a<0时,令f′(x)>0,解得:x$>\sqrt{-a}$,或x$<-\sqrt{-a}$(舍)
令f′(x)<0,解得$0<x<\sqrt{-a}$,
∴f(x)在($\sqrt{-a},+∞$)上单调递增,在(0,$\sqrt{-a}$)上单调递减.
综上所述,当a>0时,f(x)在(0,+∞)上单调递增;
当a<0时,f(x)在($\sqrt{-a},+∞$)上单调递增,在(0,$\sqrt{-a}$)上单调递减.
点评 本题考查了利用导数判断函数的单调性,渗透了分类讨论思想,是一道基础题,学生在处理这种题型时还应注意到函数的定义域.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
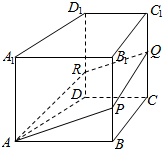 如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,∠DCB=90°,AB=AD=AA1=2DC,Q为棱CC1上一动点,过直线AQ的平面分别与棱BB1,DD1交于点P,R,则下列结论错误的是( )
如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,∠DCB=90°,AB=AD=AA1=2DC,Q为棱CC1上一动点,过直线AQ的平面分别与棱BB1,DD1交于点P,R,则下列结论错误的是( )| A. | 对于任意的点Q,都有AP∥QR | |
| B. | 对于任意的点Q,四边形APQR不可能为平行四边形 | |
| C. | 存在点Q,使得△ARP为等腰直角三角形 | |
| D. | 存在点Q,使得直线BC∥平面APQR |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 135° | C. | 120° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com