
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)(i)函数g(x)=x2+(b+3)x+2b,结合x=a是f(x)的一个极大值点,我们分析函数g(x)=x2+(b+3)x+2b的两个零点与0的关系,即可确定b的取值范围;
(ii)由函数f(x)=(x-a)2(x+b)ex,我们易求出f'(x)的解析式,由(I)可得x1、a、x2是f(x)的三个极值点,求出x1,x2,分别讨论x1、a、x2是x1,x2,x3,x4的某种排列构造等差数列时其中三项,即可得到结论.
解答 解:(1)a=0,b=-3时:
f(x)=x2(x-3)2ex,
f′(x)=exx(x-3)(x-2)(+3),
令f′(x)>0,解得:x<-3或0<x<2或x>3,
令f′(x)<0,解得:-3<x<0或2<x<3,
∴f(x)在(-∞,-3),(0,2),(3,+∞)递增,在(-3,0),(2,3)递减;
(2)(i)解:a=0时,f(x)=x2(x+b)ex,∴f'(x)=[x2(x+b)]′ex+x2(x+b)(ex)′=exx[x2+(b+3)x+2b],
令g(x)=x2+(b+3)x+2b,∵△=(b+3)2-8b=(b-1)2+8>0,∴设x1<x2是g(x)=0的两个根,
①当x1=0或x2=0时,则x=0不是极值点,不合题意;
②当x1≠0且x2≠0时,由于x=0是f(x)的极大值点,故x1<0<x2.∴g(0)<0,即2b<0,∴b<0.
(ii)解:f'(x)=ex(x-a)[x2+(3-a+b)x+2b-ab-a],
令g(x)=x2+(3-a+b)x+2b-ab-a,则△=(3-a+b)2-4(2b-ab-a)=(a+b-1)2+8>0,
于是,假设x1,x2是g(x)=0的两个实根,且x1<x2.
由(i)可知,必有x1<a<x2,且x1、a、x2是f(x)的三个极值点,
则x1=$\frac{(a-b-3)-\sqrt{{(a+b-1)}^{2}+8}}{2}$,x2=$\frac{(a-b-3)+\sqrt{{(a+b-1)}^{2}+8}}{2}$,
假设存在b及x4满足题意,
①当x1,a,x2等差时,即x2-a=a-x1时,
则x4=2x2-a或x4=2x1-a,
于是2a=x1+x2=a-b-3,即b=-a-3.
此时x4=2x2-a=a-b-3+$\sqrt{{(a+b-1)}^{2}+8}$-a=a+2$\sqrt{6}$或x4=2x1-a=a-b-3-$\sqrt{{(a+b-1)}^{2}+8}$-a=a-2$\sqrt{6}$,
②当x2-a≠a-x1时,则x2-a=2(a-x1)或(a-x1)=2(x2-a)
若x2-a=2(a-x1),则x4=$\frac{a{+x}_{2}}{2}$,
于是3a=2x1+x2=$\frac{3(a-b-3)-\sqrt{{(a+b-1)}^{2}+8}}{2}$,
即$\sqrt{{(a+b-1)}^{2}+8}$=-3(a+b+3).
两边平方得(a+b-1)2+9(a+b-1)+17=0,∵a+b+3<0,于是a+b-1=$\frac{-9-\sqrt{13}}{2}$
此时b=-a-$\frac{7+\sqrt{13}}{2}$,
此时x4=$\frac{a{+x}_{2}}{2}$=$\frac{2a+(a-b-3)-3(a+b+3)}{4}$=-b-3=a+$\frac{1+\sqrt{3}}{2}$.
②若(a-x1)=2(x2-a),则x4=$\frac{a{+x}_{1}}{2}$,
于是3a=2x2+x1=$\frac{3(a-b-3)+\sqrt{{(a+b-1)}^{2}+8}}{2}$,
即 $\sqrt{{(a+b-1)}^{2}+8}$=3(a+b+3)
两边平方得(a+b-1)2+9(a+b-1)+17=0,∵a+b+3>0,于是a+b-1=$\frac{-9+\sqrt{13}}{2}$,
此时b=-a-$\frac{7-\sqrt{13}}{2}$,此时x4=$\frac{a{+x}_{1}}{2}$$\frac{2a+(a-b-3)-3(a+b+3)}{4}$═-b-3=a+$\frac{1-\sqrt{13}}{2}$,
综上所述,存在b满足题意,
当b=-a-3时,x4=a±2$\sqrt{6}$,
b=-a-$\frac{7+\sqrt{13}}{2}$时,x4=a+$\frac{1+\sqrt{13}}{2}$,
b=-a-$\frac{7-\sqrt{13}}{2}$时,x4=a+$\frac{1-\sqrt{13}}{2}$.
点评 本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论证能力、分类讨论等综合解题能力和创新意识.


科目:高中数学 来源: 题型:选择题
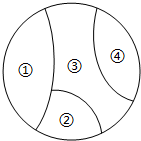 将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )
将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com