
分析 (1)在数列的前n项和中,取n=1求得a1,再由an=Sn-Sn-1(n≥2)求得an;
(2)由(1)中求得的通项公式,利用定义判断数列是等差数列.
解答 解:(1)由Sn=2n2-30n,得${a}_{1}={S}_{1}=2×{1}^{2}-30×1=-28$,
当n≥2时,an=Sn-Sn-1=2n2-30n-[2(n-1)2-30(n-1)]=4n-32.
验证n=1上式成立,
∴an=4n-32;
(2)由an=4n-32,得an-1=4(n-1)-32(n≥2),
∴an-an-1=4n-32-[4(n-1)-32]=4(常数),
∴数列{an}是等差数列.
点评 本题考查等差数列的通项公式,考查了等差数列的前n项和,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
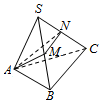 如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值.
如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-12,3] | B. | (-12,3) | C. | (-12,4] | D. | (-12,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com