
分析 (1)利用正弦函数的有界性,可得关于a的分式不等式组,求解分式不等式组得答案;
(2)化余弦为正弦,然后利用配方法求得答案.
解答 解:(1)由sinx=$\frac{a+1}{a-2}$,得-1$≤\frac{a+1}{a-2}≤1$,
即$\left\{\begin{array}{l}{\frac{a+1}{a-2}≥-1}\\{\frac{a+1}{a-2}≤1}\end{array}\right.$,解得:a$≤\frac{1}{2}$;
(2)y=cos2x+2sinx-2=-sin2x+2sinx-1=-(sin2x-2sinx+1)=-(sinx-1)2,
∵-1≤sinx≤1,
∴y=-(sinx-1)2∈[-4,0].
点评 本题考查三角函数的最值,考查了三角函数的有界性,是基础的计算题.


科目:高中数学 来源: 题型:选择题
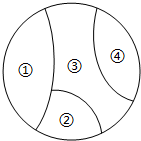 将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )
将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
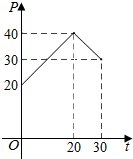 据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.
据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com