
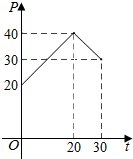
 据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.
据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.分析 (Ⅰ)通过讨论t的范围,求出函数的表达式即可;(Ⅱ)先求出函数的表达式,通过讨论t的范围,求出函数的最大值即可.
解答 解:(I)①当0≤t<20,t∈N时,
设P=at+b,将(0,20),(20,40)代入,得$\left\{\begin{array}{l}20=b\\ 40=20a+b\end{array}\right.$解得$\left\{\begin{array}{l}a=1\\ b=20.\end{array}\right.$
所以P=t+20(0≤t<20,t∈N).….(3分)
②当20≤t≤30,t∈N时,
设P=at+b,将(20,40),(30,30)代入,解得$\left\{\begin{array}{l}a=-1\\ b=60.\end{array}\right.$
所以 P=-t+60(20≤t≤30,t∈N),….(6分)
综上所述$P=\left\{\begin{array}{l}t+20(0≤t<20,t∈N)\\-t+60(20≤t≤30,t∈N).\end{array}\right.$….(7分)
(II)依题意,有y=P•Q,
得$y=\left\{\begin{array}{l}(t+20)(-t+40)(0≤t<20,t∈N)\\(-t+60)(-t+40)(20≤t≤30,t∈N).\end{array}\right.$….(9分)
化简得$y=\left\{\begin{array}{l}-{t^2}+20t+800(0≤t<20,t∈N)\\{t^2}-100t+2400(20≤t≤30,t∈N).\end{array}\right.$
整理得 $y=\left\{\begin{array}{l}-{(t-10)^2}+900(0≤t<20,t∈N)\\{(t-50)^2}-100(20≤t≤30,t∈N).\end{array}\right.$….(11分)
①当0≤t<20,t∈N时,由y=-(t-10)2+900可得,当t=10时,y有最大值900元.…(12分)
②当20≤t≤30,t∈N时,由y=(t-50)2-100可得,当t=20时,y有最大值800元.….(13分)
因为 900>800,所以在第10天时,日销售额最大,最大值为900元.….(14分)
点评 本题考查了求函数的表达式问题,考查分段函数,函数的最值问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距灯塔60海里的M处,下午2时到达这座灯塔的东偏南45°的N处,则该船航行的速度为$\frac{15\sqrt{6}}{2}$海里/小时.
如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距灯塔60海里的M处,下午2时到达这座灯塔的东偏南45°的N处,则该船航行的速度为$\frac{15\sqrt{6}}{2}$海里/小时.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com