
分析 (1)由已知利用正弦定理可得sinA=2sinC,利用诱导公式可得sinA=cosC,联立,利用同角三角函数基本关系式即可解得sinC.
(2)由(1)结合余弦定理并利用大边对大角可得c>$\frac{1}{2}$,解得c的值,利用正弦定理即可得解△ABC外接圆的半径.
解答 (本题满分为10分)
解:(1)∵a=2c,∴sinA=2sinC①,----------(1分)
又∵A-C=$\frac{π}{2}$,∴sinA=sin(C+$\frac{π}{2}$)=cosC②,----------(3分)
联立①②,即可求得cosC=$\frac{2\sqrt{5}}{5}$;sinC=$\frac{\sqrt{5}}{5}$.-----------(5分)
(2)由(1)结合余弦定理可知,c2=a2+b2-2abcosC,
可得:c2=4c2+1-2×2c×1×$\frac{2\sqrt{5}}{5}$,解得:c=$\frac{\sqrt{5}}{3}$或c=$\frac{\sqrt{5}}{5}$,---------(7分)
∵由已知易得A>$\frac{π}{2}$,
∴a>b,可得:2c>1,即:c>$\frac{1}{2}$,
∴c=$\frac{\sqrt{5}}{3}$,---------(8分)
∵2R=$\frac{c}{sinC}$=$\frac{\frac{\sqrt{5}}{3}}{\frac{\sqrt{5}}{5}}$=$\frac{5}{3}$,
∴R=$\frac{5}{6}$.----------(10分)
点评 本题主要考查了正弦定理,诱导公式,同角三角函数基本关系式,余弦定理,大边对大角在解三角形中的应用,考查了转化思想,属于基础题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,$\frac{1}{2}$] | B. | [-$\frac{2}{3}$,-$\frac{1}{2}$] | C. | [-$\frac{2}{3}$,$\frac{1}{2}$] | D. | [-$\frac{2}{3}$,$\frac{2}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(-1,3),$\overrightarrow{b}$=(2,6) | B. | $\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(4,8) | C. | $\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(3,1) | D. | $\overrightarrow{a}$=(-3,2),$\overrightarrow{b}$=(6,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
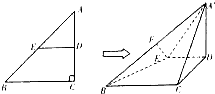 如图,在△ABC中,∠C=90°,AC=BC,D,E分别是AC,AB的中点,现将△ABC沿DE折成直二面角A′-DE-B,连接A′B,A′C,F是A′B的中点.
如图,在△ABC中,∠C=90°,AC=BC,D,E分别是AC,AB的中点,现将△ABC沿DE折成直二面角A′-DE-B,连接A′B,A′C,F是A′B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com