
| A. | k=-1 | B. | k<-1 | C. | -1≤k≤1 | D. | k≤-1 |
分析 求出集合A={y|0≤y≤1},B={y|y=kx+1,0≤x≤1},由A⊆B,列出方程组,能求出实数k的取值范围.
解答 解:∵A={y|y=x${\;}^{\frac{1}{2}}$,0≤x≤1}={y|0≤y≤1},
B={y|y=kx+1,x∈A}={y|y=kx+1,0≤x≤1},
∵A⊆B,
∴$\left\{\begin{array}{l}{k×0+1≥1}\\{k×1+1≤0}\end{array}\right.$,解得k≤-1.
∴实数k的取值范围为k≤-1.
故选:D.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意不等式的性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是圆O的直径,点C是圆O上异于A、B的点,直线度PC⊥平面ABC,E、F分别是PA、PC的中点.
如图,AB是圆O的直径,点C是圆O上异于A、B的点,直线度PC⊥平面ABC,E、F分别是PA、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都小于2 | B. | 都大于2 | ||
| C. | 至少有一个不大于2 | D. | 至少有一个不小于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
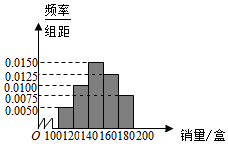 某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com