
| A. | [-$\frac{1}{2}$,+∞) | B. | (0,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,+∞] | D. | (0,$\frac{1}{2}$] |
分析 不等式即$\left\{\begin{array}{l}{2x+1≥0}\\{x+1≥0}\\{\sqrt{2x+1}+1>\sqrt{x+1}}\end{array}\right.$,即 $\left\{\begin{array}{l}{x≥-\frac{1}{2}}\\{2\sqrt{2x+1}>-x-1}\end{array}\right.$,由此求得x的范围.
解答 解:由不等式$\sqrt{2x+1}$>$\sqrt{x+1}$-1,可得$\left\{\begin{array}{l}{2x+1≥0}\\{x+1≥0}\\{\sqrt{2x+1}+1>\sqrt{x+1}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x≥-\frac{1}{2}}\\{2x+1+2\sqrt{2x+1}+1>x+1}\end{array}\right.$,即 $\left\{\begin{array}{l}{x≥-\frac{1}{2}}\\{2\sqrt{2x+1}>-x-1}\end{array}\right.$ ①.
由于当x≥-$\frac{1}{2}$时,-x-1<0,2$\sqrt{2x+1}$>-x-1恒成立,
解得①的解为 x≥-$\frac{1}{2}$,
故选:A.
点评 本题主要考查根式不等式的解法,体现了等价转化的数学思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 4+2$\sqrt{6}$ | C. | 4+2$\sqrt{3}$ | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
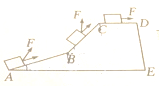 如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.
如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com