
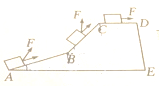
 ��ͼ��ʾ��һ������б��������F����������A��B��C�˶���D������AB=50m��BC=40m��CD=30m������F=$\left\{\begin{array}{l}{\frac{1}{4}x+5��0��x��90}\\{20��x��90}\end{array}\right.$������xΪ���룬��λ��m������F�ĵ�λ��N������AB���˶�ʱF���˶������30��ǣ���BC���˶�ʱF���˶������45�㣬��CD��F���˶�������ͬ����������A�˶���D����F�����Ĺ�W��
��ͼ��ʾ��һ������б��������F����������A��B��C�˶���D������AB=50m��BC=40m��CD=30m������F=$\left\{\begin{array}{l}{\frac{1}{4}x+5��0��x��90}\\{20��x��90}\end{array}\right.$������xΪ���룬��λ��m������F�ĵ�λ��N������AB���˶�ʱF���˶������30��ǣ���BC���˶�ʱF���˶������45�㣬��CD��F���˶�������ͬ����������A�˶���D����F�����Ĺ�W�� ���� ���������F�������˶�����ķ�������AB��ʱ������ΪFcos30�㣻��BC��ʱ������ΪFcos45�㣬�������ݱ��������Ĺ�ʽ���ɵõ�A��D����F����W=${{��}_{0}}^{50}��\frac{1}{4}x+5��cos30��$dx+${{��}_{50}}^{90}��\frac{1}{4}x+5��cos45��dx+600$�����Խ��ж����ֵļ��㼴�ɣ�
��� �⣺��AB���˶�ʱF���˶�����ķ���F1=Fcos30�㣬��BC���˶�ʱF���˶�����ķ���F2=Fcos45�㣻
�ɱ���������ʽ�ã�
W=${{��}_{0}}^{50}��\frac{1}{4}x+5��cos30��dx+$${{��}_{50}}^{90}��\frac{1}{4}x+5��cos45��dx$+600=$\frac{\sqrt{3}}{2}��\frac{1}{8}{x}^{2}+5x��{{|}_{0}}^{50}$$+\frac{\sqrt{2}}{2}��\frac{1}{8}{x}^{2}+5x��{{|}_{50}}^{90}+600$=$\frac{1125\sqrt{3}}{4}+450\sqrt{2}+600$��
���� �����ö���������������ķ��������㹫ʽ���Լ������ֵļ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{1}{2}$��+�ޣ� | B�� | ��0��$\frac{1}{2}$�� | C�� | ��$\frac{1}{2}$��+��] | D�� | ��0��$\frac{1}{2}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����f��x��������[1��2]����[2��3]����һ����� | |
| B�� | ����f��x��������[1��2]��[2��3]�ϸ���һ����� | |
| C�� | ����f��x��������[1��3]�������������� | |
| D�� | ����f��x��������[1��3]���������������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {0��1��2} | B�� | {0��1��2��3} | C�� | {-2��-1��0} | D�� | {-1��0��1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com