
分析 根据平面向量基本定理求出m,n关系,进而确定$\frac{1}{m}$+$\frac{1}{n}$取最小值时m,n的值,代入求$\overrightarrow{a}$的模.
解答  解:∵$\overrightarrow{AC}=4\overrightarrow{AE}$,∴$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$=m$\overrightarrow{AB}$+4n$\overrightarrow{AE}$,
解:∵$\overrightarrow{AC}=4\overrightarrow{AE}$,∴$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$=m$\overrightarrow{AB}$+4n$\overrightarrow{AE}$,
又∵P为BE上一点,不妨设$\overrightarrow{BP}=λ\overrightarrow{BE}$(0<λ<1),
∴$\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{BP}$=$\overrightarrow{AB}$+λ$\overrightarrow{BE}$=$\overrightarrow{AB}$+λ($\overrightarrow{AE}-\overrightarrow{AB}$)=(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AE}$,
∴m$\overrightarrow{AB}$+4n$\overrightarrow{AE}$=(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AE}$,
∵$\overrightarrow{AB}$,$\overrightarrow{AE}$不共线,
∴$\left\{\begin{array}{l}{m=1-λ}\\{4n=λ}\end{array}\right.$,所以m+4n=1-λ+λ=1
∴$\frac{1}{m}$$+\frac{1}{n}$=($\frac{1}{m}+\frac{1}{n}$)×(m+4n)=5+4$\frac{n}{m}$+$\frac{m}{n}$
≥5+2$\sqrt{\frac{4n}{m}×\frac{m}{n}}$=9(m>0,n>0)
当且仅当$\frac{4n}{m}=\frac{m}{n}$即m=2n时等号成立,
又∵m+4n=1,∴m=$\frac{1}{3}$,n=$\frac{1}{6}$,
∴|$\overrightarrow{a}$|=$\sqrt{{m}^{2}+{n}^{2}}$=$\frac{\sqrt{5}}{6}$,
故答案为:$\frac{\sqrt{5}}{6}$.
点评 本题考查平面向量基本定理和基本不等式求最值,难点在于利用向量求m,n的关系和求$\frac{1}{m}$+$\frac{1}{n}$的最值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
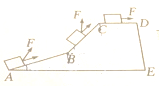 如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.
如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 沿x轴方向向右平移$\frac{π}{4}$ | B. | 沿x轴方向向右平移$\frac{π}{12}$ | ||
| C. | 沿x轴方向向左平移$\frac{π}{4}$ | D. | 沿x轴方向向左平移$\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | E(2X-1)=2np | B. | D(2X+1)=4np(1-p)+1 | C. | E(2X+1)=4np+1 | D. | D(2X-1)=4np(1-p) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | (300,+∞) |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 100 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.025 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com