
分析 由条件利用诱导公式,二倍角公式求得${sin}^{2}(\frac{π}{4}-x)$ 的值,再根据x为钝角,可得sin(${\frac{π}{4}$-x)<0,从而求得sin(${\frac{π}{4}$-x)的值.
解答 解:由于sin2x=-$\frac{7}{25}$=-cos(2x+$\frac{π}{2}$)=1-2${cos}^{2}(x+\frac{π}{4})$=1-2${sin}^{2}(\frac{π}{4}-x)$,
∴${sin}^{2}(\frac{π}{4}-x)$=$\frac{16}{25}$.
再根据0<x<π,且sin2x=-$\frac{7}{25}$=2sinxcosx,可得x为钝角,
∴$\frac{π}{4}$-x∈(-$\frac{3π}{4}$,-$\frac{π}{4}$),∴sin(${\frac{π}{4}$-x)<0,∴sin(${\frac{π}{4}$-x)=-$\frac{4}{5}$,
故答案为:$-\frac{4}{5}$.
点评 本题主要考查诱导公式,二倍角公式的应用,三角函数在各个象限中的符号,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 4+2$\sqrt{6}$ | C. | 4+2$\sqrt{3}$ | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
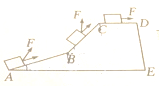 如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.
如图所示,一物体沿斜面在拉力F的作用下由A经B,C运动到D,其中AB=50m,BC=40m,CD=30m,变力F=$\left\{\begin{array}{l}{\frac{1}{4}x+5,0≤x≤90}\\{20,x>90}\end{array}\right.$(其中x为距离,单位:m,变力F的单位:N),在AB段运动时F与运动方向成30°角,在BC段运动时F与运动方向成45°,在CD段F与运动方向相同,求物体由A运动到D变力F所作的功W.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com