
如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=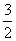 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
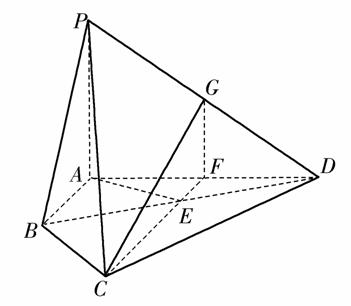
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
科目:高中数学 来源: 题型:
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
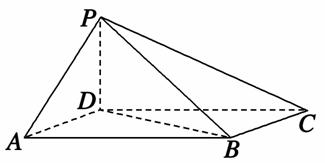
(1)证明:PA⊥BD;
(2)设PD=AD,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点M是直线l:2x-y-4=0与x轴的交点,把直线l绕点M按逆时针方向旋转45°,得到的直线方程是( )
A.3x+y-6=0 B.3x-y+6=0
C.x+y-3=0 D.x-3y-2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是( )
A.[-3,-1] B.[-1,3]
C.[-3,1] D.(-∞,-3]∪[1,+∞)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市石景山区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
函数 的定义域为
的定义域为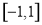 ,图象如图1所示;函数
,图象如图1所示;函数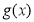 的定义域为
的定义域为 ,图象如图2所示,方程
,图象如图2所示,方程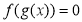 有
有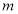 个实数根,方程
个实数根,方程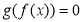 有
有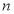 个实数根,则
个实数根,则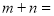 ( )
( )
A.6 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com