
| A. | 7 | B. | 6 | C. | 3 | D. | 2 |
分析 根据f(x)的对称性和奇偶性可知f(x)在[-$\frac{1}{2}$,$\frac{5}{2}$]上共有3条对称轴,x=0,x=1,x=2,根据三角函数的对称性可知y=|cos(πx)|也关于x=0,x=1,x=2对称,故而g(x)在[-$\frac{1}{2}$,$\frac{5}{2}$]上3条对称轴,根据f(x)和y=|cos(πx)|在[0,1]上的函数图象,判断g(x)在[-$\frac{1}{2}$,$\frac{5}{2}$]上的零点分布情况,利用函数的对称性得出零点之和.
解答 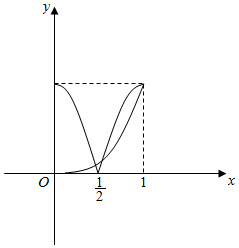 解:∵f(x)=f(2-x),∴f(x)关于x=1对称,
解:∵f(x)=f(2-x),∴f(x)关于x=1对称,
∵f(-x)=f(x),∴f(x)根与x=0对称,
∵f(x)=f(2-x)=f(x-2),∴f(x)=f(x+2),
∴f(x)是以2为周期的函数,
∴f(x)在[-$\frac{1}{2}$,$\frac{5}{2}$]上共有3条对称轴,分别为x=0,x=1,x=2,
又y=|cos(πx)关于x=0,x=1,x=2对称,
∴x=0,x=1,x=2为g(x)的对称轴.
作出y=|cos(πx)|和y=x3在[0,1]上的函数图象如图所示:
由图象可知g(x)在(0,$\frac{1}{2}$)和($\frac{1}{2}$,1)上各有1个零点.
又g(1)=0,∴g(x)在[-$\frac{1}{2}$,$\frac{5}{2}$]上共有7个零点,
设这7个零点从小到大依次为x1,x2,x3,…x6,x7.
则x1,x2关于x=0对称,x3,x5关于x=1对称,x4=1,x6,x7关于x=2对称.
∴x1+x2=0,x3+x5=2,x6+x7=4,
∴x1+x2+x3+x4+x5+x6+x7=7.
故选:A.
点评 本题考查了函数的周期性,奇偶性的应用,函数零点个数判断,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
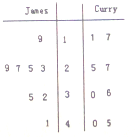 如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )
如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )| A. | 他们的水平相当,但James 比Curry发挥稳定 | |
| B. | 他们的水平相当,但Curry比James 发挥稳定 | |
| C. | James比Curry水平高,也比Curry发挥稳定 | |
| D. | Curry比水平高,也比James发挥稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4<a≤0 | B. | a<-4 | C. | -4<a<0 | D. | a≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com