练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．如图，已知正方形的面积为100，向正方形内随机地撒200颗黄豆，数得落在阴影外的黄豆数为114颗，以此实验数据为依据，可以估计出阴影部分的面积约为（　　）
    A．53B．43C．47D．57

    分析 本题利用几何概型求解．由于是向正方形内随机地撒200颗黄豆，其落在阴影外的概率是阴影外的面积与整个正方形的面积之比，从而可列式求得阴影部分的面积．

    解答 解：设阴影外部分的面积为s，
    则由几何概型的概率公式得：$\frac{s}{100}=\frac{114}{200}$，
    解得s=57，
    可以估计出阴影部分的面积约为100-57=43．
    故选：B．

    点评 本题主要考查了几何概型，以及利用几何意义求面积，属于基础题．简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

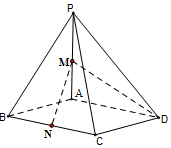    9．如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠ABC=$\frac{π}{3}$，PA⊥底面ABCD，PA=AB=2，M为PA的中点，N为BC的中点
    （1）证明：直线MN∥平面PCD；
    （2）求异面直线AB与MD所成角的余弦值；
    （3）求点B到平面PCD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=$\frac{{x}^{2}}{1+{x}^{2}}$+log2x．
    （1）求f（2），f（$\frac{1}{2}$），f（4），f（$\frac{1}{4}$）的值，并计算f（2）+f（$\frac{1}{2}$），f（4）+f（$\frac{1}{4}$）；
    （2）求f（1）+f（2）+f（3）+…+f（2016）+f（$\frac{1}{2}$）+f（$\frac{1}{3}$）+…f（$\frac{1}{2016}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列各组中的两个函数是相等函数的为（　　）
    A．y=x2-2x-1与y=t2-2t-1B．y=1与 $y=\frac{x}{x}$
    C．y=6x与$y=6\sqrt{x^2}$D．$y={（\sqrt{x}）^2}$与$y=\root{3}{x^3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知点F1（-4，0），F2（4，0），动点P满足|PF2|-|PF1|=4，则动点P的轨迹方程为$\frac{x^2}{4}-\frac{y^2}{12}=1（x≤-2）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列选项中叙述错误的是（　　）
    A．若“p∧q”为假命题，则“p∨q”为真命题
    B．命题“若m2+n2=0，则m=0且n=0”的否命题是“若m2+n2≠0，则m≠0或n≠0”
    C．命题“若x=0，则x2-x=0”的逆否命题为真命题
    D．若命题p：?n∈N，n2＞2n，则?p：?n∈N，n2≤2n

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=lnx+$\frac{a}{x}$（a∈R）
    （1）讨论函数f（x）的单调性；
    （2）当a=2时，求函数f（x）在区间[1，e]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

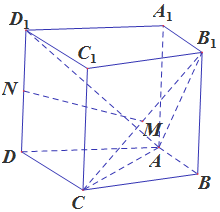    8．如图，在四棱柱ABCD-A1B1C1D1中，侧棱A1A⊥底面ABCD，AB⊥AC，AB=1，AC=AA1=2，AD=CD=$\sqrt{5}$，且点M和N分别为B1C和D1D的中点．
    （I）求证：MN∥平面ABCD；
    （II）求二面角D1-AC-B1的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．给出下列命题：①存在实数x，使$sinx+cosx=\frac{3}{2}$；②若α，β是第一象限角，且α＞β，则cosα＞cosβ；③函数$y=sin（\frac{2}{3}x+\frac{π}{2}）$是偶函数；④函数y=sin2x的图象向左平移$\frac{π}{4}$个单位，得到函数$y=sin（2x+\frac{π}{4}）$的图象．
    其中正确命题的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    同步练习册答案