
分析 (1)求出函数的导数,通过讨论a的范围,得到函数的单调区间;
(2)a=2时,求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的最大值和最小值即可.
解答 解:(1)f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$ (x>0)(2分)
①当a≤0时,f′(x)>0,f(x)在区间(0,+∞)上单调递增,
②当a>0时,在区间(0,a)上,f′(x)<0,f(x)单调递减;
在区间(a,+∞)上,f′(x)>0,f(x)单调递增.(5分)
综上可知:当a≤0时,f(x)在区间(0,+∞)上单调递增.
当a>0时,在区间(0,a)上,f(x)单调递减;
在区间(a,+∞)上,f(x)单调递增.(7分)
(2)当a=2时,f(x)=lnx+$\frac{2}{x}$,f′(x)=$\frac{1}{x}$-$\frac{2}{{x}^{2}}$,
令f′(x)=0,得x=2
| x | 1 | (1,2) | 2 | (2,e) | e |
| f′(x) | -1 | - | 0 | + | $\frac{e-2}{{e}^{2}}$ |
| f(x) | 2 | 减 | 极小值 | 增 | 1+$\frac{2}{e}$ |
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知正方形的面积为100,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )
如图,已知正方形的面积为100,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )| A. | 53 | B. | 43 | C. | 47 | D. | 57 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
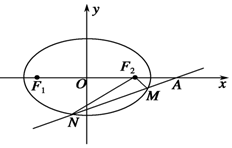 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$.以原点为圆心,椭圆的短轴长为直径的圆与直线x-y+$\sqrt{2}$=0相切.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$.以原点为圆心,椭圆的短轴长为直径的圆与直线x-y+$\sqrt{2}$=0相切.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [$\frac{4}{3}$,+∞) | C. | [0,$\frac{4}{3}$] | D. | (0,$\frac{4}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com