
分析 先根据条件得到函数的奇偶性,再结合条件求出函数在[-1,1]上的单调性,最后根据单调性建立关系式求解即可.
解答 解:∵函数f(x)满足f(-x)=-f(x),
∴函数f(x)是奇函数.
又∵当a,b∈[-1,0)时,总有$\frac{f(a)-f(b)}{a-b}$>0,
∴函数f(x)在[-1,0)上单调递增函数
根据奇函数的性质可知函数f(x)在[-1,1]上单调递增函数
∵f(m+1)>f(2m),
∴-1≤2m<m+1≤1,
∴$-\frac{1}{2}≤m≤0$.
故答案为$-\frac{1}{2}≤m≤0$.
点评 本题主要考查了函数的单调性的应用,以及函数奇偶性的应用,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:解答题
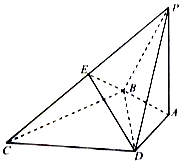 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,△BCD为等边三角形,PA=BD=$\sqrt{3}$,AB=AD,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,△BCD为等边三角形,PA=BD=$\sqrt{3}$,AB=AD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2-2x-1与y=t2-2t-1 | B. | y=1与 $y=\frac{x}{x}$ | ||
| C. | y=6x与$y=6\sqrt{x^2}$ | D. | $y={(\sqrt{x})^2}$与$y=\root{3}{x^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若“p∧q”为假命题,则“p∨q”为真命题 | |
| B. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0” | |
| C. | 命题“若x=0,则x2-x=0”的逆否命题为真命题 | |
| D. | 若命题p:?n∈N,n2>2n,则?p:?n∈N,n2≤2n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,角A,B,C的对边分别是a,b,c,则a>b是cos A<cos B的充要条件 | |
| B. | 命题p:对任意的x∈R,x2+x+1>0,则¬p:对任意的x∈R,x2+x+1≤0 | |
| C. | 已知p:$\frac{1}{x+1}$>0,则¬p:$\frac{1}{x+1}$≤0 | |
| D. | 存在实数x∈R,使sin x+cos x=$\frac{π}{2}$成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
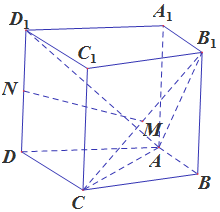 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com