
分析 (1)由已知求出圆的半径,得到圆的方程,求出A,B的坐标,代入三角形面积公式得答案;
(2)由|OM|=|ON|,可得OC垂直平分线段MN,求出直线OC的方程,得到OC的斜率,利用斜率的关系求得t值,可得圆C的标准方程.
解答 解:(1)∵圆C过原点O,∴$O{C^2}={t^2}+\frac{4}{t^2}$,即圆C标准方程为${(x-t)^2}+{(y-\frac{2}{t})^2}={t^2}+\frac{4}{t^2}$.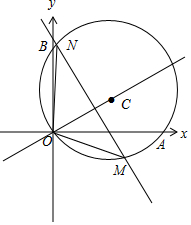
令x=0,得y1=0,${y_2}=\frac{4}{t}$;令y=0,得x1=0,x2=2t.
∴${S_{△OAB}}=\frac{1}{2}OA•OB=\frac{1}{2}|{\frac{4}{t}}|•|{2t}|=4$,即△OAB的面积为定值4;
(2)∵|OM|=|ON|,∴OC垂直平分线段MN,直线OC的方程为$y=\frac{1}{2}x$,
即$\frac{2}{t}=\frac{1}{2}t$,得t=2或t=-2.
当t=2时,满足题意;当t=-2时,直线y=-2x+4与圆C不相交,舍去.
∴圆C的标准方程为(x-2)2+(y-1)2=5.
点评 本题考查圆的标准方程,考查直线与圆位置关系的应用,考查两直线垂直与斜率的关系,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 任何事件的概率总是在(0,1]之间 | |
| B. | 频率是客观存在的,与试验次数无关 | |
| C. | 随着试验次数的增加,事件发生的频率一般会稳定于概率 | |
| D. | 概率是随机的,在试验前不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | $({1,\sqrt{3}})$ | C. | $({\sqrt{3},2})$ | D. | $({\sqrt{3},\sqrt{5}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com