
分析 (1)a=$\frac{p}{2}$时,设过点M的直线l为x=ty+$\frac{p}{2}$,与抛物线方程联立消去x,得关于y的一元二次方程,由根与系数的关系和数量积的坐标运算即可求出$\overrightarrow{OA}$•$\overrightarrow{OB}$为定值;
(2)设出直线AB的方程为x=ty+n,与抛物线方程联立消去x,得关于y的一元二次方程,由根与系数的关系得出y1y2的值,再由题意列出方程求出n的值,即可得出直线AB过定点;
(3)由题意写出直线AB的方程为y=x-a,与抛物线方程联立消去y,得关于x的一元二次方程,由根与系数的关系以及判别式△>0,即可求出a的取值范围.
解答 解:(1)当a=$\frac{p}{2}$时,点M($\frac{p}{2}$,0),
设直线l:x=ty+$\frac{p}{2}$,
由$\left\{\begin{array}{l}{{y}^{2}=2px}\\{x=ty+\frac{p}{2}}\end{array}\right.$,消去x,得
y2-2pty-p2=0,…2分
所以y1y2=-p2,
则x1x2=$\frac{{{y}_{1}}^{2}{{•y}_{2}}^{2}}{{4p}^{2}}$=$\frac{{p}^{2}}{4}$;…4分
$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=$\frac{{p}^{2}}{4}$-p2=-$\frac{{3p}^{2}}{4}$为定值;…5分
(2)设直线AB:x=ty+n,
由$\left\{\begin{array}{l}{{y}^{2}=2px}\\{x=ty+n}\end{array}\right.$,消去x,得
y2-2pty-2pn=0,…7分
所以y1y2=-2pn,
又y1•y2=m,则-2pn=m,即n=-$\frac{m}{2p}$;…9分
则直线AB过定点(-$\frac{m}{2p}$,0);…10分
(3)由题意:直线AB的方程为:y=x-a,
代入抛物线得:x2-2(a+p)x+a2=0,
由△=4(a+p)2-4a2>0得:a>-$\frac{p}{2}$;…13分
x1+x2=2(a+p),x1x2=a2,
所以|AB|=$\sqrt{2}$|x1-x2|=2$\sqrt{2}$$\sqrt{2ap{+p}^{2}}$≤2p,
解得a≤-$\frac{p}{4}$;…15分
所以a的取值范围是(-$\frac{p}{2}$,-$\frac{p}{4}$]…16分.
点评 本题考查了直线与抛物线方程的应用问题,也考查了直线过定点以及弦长公式的应用问题,考查了二元二次方程组的应用问题,是综合性题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{21}$ | B. | $\frac{1}{21}$ | C. | $\frac{1}{14}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
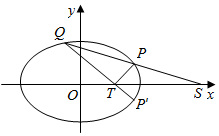 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为(-2,0),离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左顶点为(-2,0),离心率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,α∥β,则l∥β | B. | 若l⊥α,α∥β,则l⊥β | C. | 若l⊥α,α⊥β,则l∥β | D. | 若l∥α,α⊥β,则l⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com