
| A. | $({-∞,\frac{1}{4}}]$ | B. | $[{\frac{1}{4},+∞})$ | C. | $[{\frac{1}{2},+∞})$ | D. | $({-∞,\frac{1}{2}}]$ |
分析 分类参数得a≤$\frac{{e}^{x+y-2}+{e}^{x-y-2}+2}{4x}$,先把x看作常数,求出右侧函数的最小值,再把最小值看作关于x的函数,求出最小值,即可得出a的范围.
解答 解:∵ex+y-2+ex-y-2+2-4ax≥0恒成立,∴a≤$\frac{{e}^{x+y-2}+{e}^{x-y-2}+2}{4x}$恒成立,
把x看作常数,令f(y)=$\frac{{e}^{x+y-2}+{e}^{x-y-2}+2}{4x}$,则f′(y)=$\frac{{e}^{x+y-2}-{e}^{x-y-2}}{4x}$=$\frac{{e}^{x-2}({e}^{y}-{e}^{-y})}{4x}$≥0,
∴f(y)在[0,+∞)上是增函数,
∴当y=0时,f(y)取得最小值f(0)=$\frac{{e}^{x-2}+1}{2x}$,
再令g(x)=$\frac{{e}^{x-2}+1}{2x}$,则g′(x)=$\frac{{e}^{x-2}•2x-2({e}^{x-2}+1)}{4{x}^{2}}$=$\frac{{e}^{x-2}(x-1)-1}{2{x}^{2}}$,
令g′(x)=0得x=2,
∴当0<x<2时,g′(x)<0,当x>2时,g′(x)>0,
∴g(x)在(0,2)上单调递减,在(2,+∞)上单调递增,
∴当x=2时,g(x)取得最小值g(2)=$\frac{1}{2}$,
∴a$≤\frac{1}{2}$.
故选:D.
点评 本题考查了函数恒成立问题,函数单调性与最值的计算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
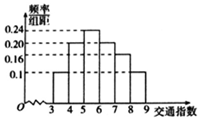 随着社会发展,广州市在一天的上下班时段经常会出现堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10)严重拥堵.早高峰时段(T≥3),从广州市交通指挥中心随机选取了50个交通路段进行调查,依据交通指数数据绘制的直方图如图所示:
随着社会发展,广州市在一天的上下班时段经常会出现堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10)严重拥堵.早高峰时段(T≥3),从广州市交通指挥中心随机选取了50个交通路段进行调查,依据交通指数数据绘制的直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
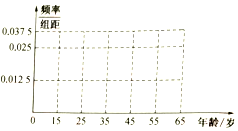 随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查40人,并将调查情况进行整理后制成如表:
随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查40人,并将调查情况进行整理后制成如表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 10 | 5 | 10 |
| 赞成人数 | 4 | 6 | 8 | 4 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
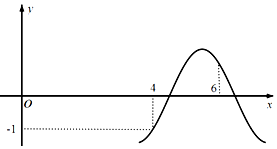
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com