
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
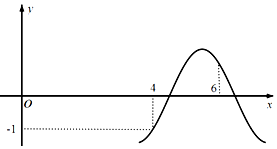
分析 根据图象经过的点以及自变量4,6的函数值关系分别求出ω,φ,A,然后求值.
解答 解:因为f(x)=Asin(ωx+φ)的部分图象,f(4)=-f(6)=-1,得到周期为T=2(6-4)=4,所以$ω=\frac{2π}{4}=\frac{π}{2}$,且$f(\frac{1}{2})=0$,所以Asin($\frac{π}{4}$+φ)=0,得到φ=$-\frac{π}{4}$,
又f(4)=-1,所以Asin(2$π-\frac{π}{4}$)=-1,解得A=$\sqrt{2}$,所以f(x)=$\sqrt{2}$sin($\frac{π}{2}x-\frac{π}{4}$)
所以f(2017)=f(504×4+1)=f(1)=$\sqrt{2}$sin($\frac{π}{2}-\frac{π}{4}$)=$\sqrt{2}×\frac{\sqrt{2}}{2}$=1;
故选C.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定解析式,考查数形结合思想,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{3}}]∪[{2,+∞}]$ | B. | $({-∞,-\frac{1}{3}}]∪[{\frac{1}{4},+∞})$ | C. | $({-∞,\frac{1}{4}}]∪[{\frac{9}{4},+∞})$ | D. | $({-∞,-\frac{1}{3}}]∪[{\frac{9}{4},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,\frac{1}{4}}]$ | B. | $[{\frac{1}{4},+∞})$ | C. | $[{\frac{1}{2},+∞})$ | D. | $({-∞,\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1,p2,p3 | B. | p1,p2,p4 | C. | p1,p3,p4 | D. | p2,p3,p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )| A. | $\sqrt{6}-1$ | B. | $\sqrt{6}$ | C. | $\sqrt{6}+1$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com