
 如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )
如图,三角形ABC中,AB=1,$BC=\sqrt{3}$,以C为直角顶点向外作等腰直角三角形ACD,当∠ABC变化时,线段BD的长度最大值为( )| A. | $\sqrt{6}-1$ | B. | $\sqrt{6}$ | C. | $\sqrt{6}+1$ | D. | $2\sqrt{3}$ |
分析 设∠ABC=α,∠ACB=β,求出AC,sinβ,利用余弦定理,即可求出对角线BD的最大值.
解答 解:设∠ABC=α,∠ACB=β,则AC2=4-2$\sqrt{3}$cosα,
由正弦定理可得sinβ=$\frac{sinα}{\sqrt{4-2\sqrt{3}cosα}}$,
∴BD2=3+4-2$\sqrt{3}$cosα-2×$\sqrt{3}$×$\sqrt{4-2\sqrt{3}cosα}$×cos(90°+β)=7-2$\sqrt{3}$cosα+2sinα=7+2$\sqrt{6}$sin(α-45°),
∴α=135°时,BD取得最大值$\sqrt{6}$+1.
故选:C
点评 本题考查余弦定理、正弦定理的运用,考查辅助角公式的运用,考查学生的计算能力,有难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
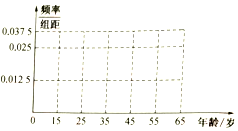 随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查40人,并将调查情况进行整理后制成如表:
随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查40人,并将调查情况进行整理后制成如表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 10 | 5 | 10 |
| 赞成人数 | 4 | 6 | 8 | 4 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
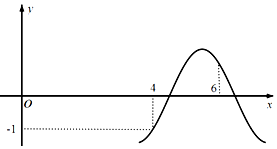
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com