练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．某工厂的污水处理程序如下：原始污水必先经过A系统处理，处理后的污水（A级水）达到环保标准（简称达标）的概率为p（0＜p＜1）．经化验检测，若确认达标便可直接排放；若不达标则必须进行B系统处理后直接排放．
    某厂现有4个标准水量的A级水池，分别取样、检测．多个污水样本检测时，既可以逐个化验，也可以将若干个样本混合在一起化验．混合样本中只要有样本不达标，则混合样本的化验结果必不达标．若混合样本不达标，则该组中各个样本必须再逐个化验；若混合样本达标，则原水池的污水直接排放．
    现有以下四种方案，
    方案一：逐个化验；
    方案二：平均分成两组化验；
    方案三：三个样本混在一起化验，剩下的一个单独化验；
    方案四：混在一起化验．
    化验次数的期望值越小，则方案的越“优”．
    （Ⅰ） 若$p=\frac{2}{{\sqrt{5}}}$，求2个A级水样本混合化验结果不达标的概率；
    （Ⅱ） 若$p=\frac{2}{{\sqrt{5}}}$，现有4个A级水样本需要化验，请问：方案一，二，四中哪个最“优”？
    （Ⅲ） 若“方案三”比“方案四”更“优”，求p的取值范围．

    分析 （Ⅰ）计算2个A级混合样本达标的概率，再根据对立事件原理求得它们不达标的概率；
    （II）计算方案一：逐个检测，检测次数为ξ=4；
    方案二：检测次数为ξ2，则ξ2可能取值为2，4，6，求概率分布列，计算数学期望；
    方案四：混在一起检测，检测次数为ξ4，则ξ4可取值为1，5，求概率分布列，计算数学期望；
    比较得出选择方案几最“优”；
    （III）方案三：化验次数为η3，则η3可取值为2，5，求概率分布列，计算数学期望；
    方案四：化验次数为η4，则η4可取值为1，5，求概率分布，计算数学期望；
    由题意列不等式E（η3）＜E（η4），求出p的取值范围．

    解答 解：（Ⅰ）2个A级混合样本达标的概率是${（{\frac{2}{{\sqrt{5}}}}）^2}=\frac{4}{5}$，…（2分）
    所以根据对立事件原理，2个A级混合样本不达标的概率为$1-\frac{4}{5}=\frac{1}{5}$；…（4分）
    （II）方案一：逐个检测，检测次数为ξ=4；
    方案二：由（I）知，每组2个样本的检测时，若达标则检测次数为1，概率为$\frac{4}{5}$；
    若不达标则检测次数为3，概率为$\frac{1}{5}$；
     故方案二的检测次数为ξ2，则ξ2可能取值为2，4，6；
    其概率分布列如下，

    ξ2246
    P${（{\frac{4}{5}}）^2}$$C_2^1×\frac{1}{5}×\frac{4}{5}$${（{\frac{1}{5}}）^2}$
    可求得方案二的期望为$E（{ξ_2}）=2×\frac{16}{25}+4×\frac{8}{25}+6×\frac{1}{25}=\frac{70}{25}$；…（6分）
    方案四：混在一起检测，记检测次数为ξ4，
    则ξ4可取值为1，5；其概率分布列如下：
    ξ415
    P${（{\frac{2}{{\sqrt{5}}}}）^4}$$1-{（{\frac{2}{{\sqrt{5}}}}）^4}$
    可求得方案四的期望为$E（{ξ_4}）=1×\frac{16}{25}+5×\frac{9}{25}=\frac{61}{25}$，…（8分）
    比较可得E（ξ4）＜E（ξ2）＜4，故选择方案四最“优”；…（9分）
    （III）方案三：设化验次数为η3，则η3可取值为2，5；
    其概率分布为：
    η325
    Pp31-p3
    数学期望为$E（{η_3}）=2•{p^3}+5（{1-{p^3}}）=5-3{p^3}$；…（10分）
    方案四：设化验次数为η4，则η4可取值为1，5；
    其概率分布为：
    η415
    Pp41-p4
    数学期望为$E（{η_4}）=1•{p^4}+5（{1-{p^4}}）=5-4{p^4}$；…（11分）
    由题意得E（η3）＜E（η4），所以5-3p3＜5-4p4，解得p＜$\frac{3}{4}$；
    所以当$0＜p＜\frac{3}{4}$时，方案三比方案四更“优”…（12分）

    点评 本题考查了离散型随机变量的概率分布列与数学期望的应用问题，是概率分布中较难的题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．已知$\overrightarrow a=（1\;，\;3）$，$\overrightarrow b=（-2\;，\;5）$，则$3\overrightarrow a-2\overrightarrow b$=（　　）
    A．（2，7）B．（13，-7）C．（7，-1）D．（-1，-1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．直线$\left\{\begin{array}{l}{x=-1+t}\\{y=9-t}\end{array}\right.$（t为参数）被圆$\left\{\begin{array}{l}{x=5cosθ+3}\\{y=5sinθ-1}\end{array}\right.$（θ为参数）所截得的弦长为$2\sqrt{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．佳佳同学在8次测试中，数学成绩的茎叶图如图，则这8次成绩的中位数是（　　）
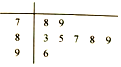
    A．86B．87C．87.5D．88.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．随机变量X服从正态分布（3，σ2），且P（X≤4）=0.84，则P（2＜X＜4）=（　　）
    A．0.16B．0.32C．0.68D．0.84

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．如图，三角形ABC中，AB=1，$BC=\sqrt{3}$，以C为直角顶点向外作等腰直角三角形ACD，当∠ABC变化时，线段BD的长度最大值为（　　）
    A．$\sqrt{6}-1$B．$\sqrt{6}$C．$\sqrt{6}+1$D．$2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．各项均为正数的等差数列{an}中，前n项和为Sn，当n∈N*，n≥2时，有${S_n}=\frac{n}{n-1}（{a_n}^2-{a_1}^2）$，则S20-2S10=50．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．复数$\frac{2}{1-i}$=（　　）
    A．$\sqrt{2}$+$\sqrt{2}$iB．$\frac{{\sqrt{2}}}{2}$+$\frac{{\sqrt{2}}}{2}$iC．1-iD．1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．若在△ABC中，sinA：sinB：sinC=3：5：6，则sinB等于（　　）
    A．$\frac{{2\sqrt{14}}}{9}$B．$\frac{{\sqrt{14}}}{9}$C．$\frac{{\sqrt{11}}}{5}$D．$\frac{{2\sqrt{11}}}{5}$

    查看答案和解析>>

    同步练习册答案