
分析 设A(x1,y1),B(x2,y2),联立x2=4y与y=kx+a有x2-4kx-4a=0,
则△=16(k2+a)>0,且x1+x2=4k,x1•x2=-4a.
(Ⅰ)由抛物线的定义有|AF|=y1+1,|BF|=y2+1,则|AD|=|AF|-1=y1,|BE|=|BF|-1=y2,
|AD|•|BE|=y1y2=(kx1+1)(kx2+1)=${k^2}{x_1}{x_2}+k({{x_1}+{x_2}})+1=-4{k^2}+4{k^2}+1=1$,即可;
(Ⅱ)当直线l的斜率为0,且Q(0,3a)时APBQ为菱形.理由如下
方法一:设A(x1,y1),B(x2,y2),Q(0,y0),若APBQ为菱形,可得${y_1}-{y_0}=\frac{1}{2}{x_1}{x_2},{y_2}-{y_0}=\frac{1}{2}{x_1}{x_2}$,
则y1=y2,∴k=0,∴$A({-2\sqrt{a},a}),B({2\sqrt{a},a})$,
则抛物线C在$A({-2\sqrt{a},a})$处的切线为$y=-\sqrt{a}x-a$,抛物线C在$B({2\sqrt{a},a})$处的切线为$y=\sqrt{a}x-a$
可得P(0,-a),又AB的中点为R(0,a),所以Q(0,3a)
方法二:设A(x1,y1),B(x2,y2),Q(0,y0),由x2=4y有$y=\frac{1}{4}{x^2}$,则$y'=\frac{1}{2}x$,
若APBQ为菱形,则${y_1}-{y_0}=\frac{1}{2}{x_1}{x_2},{y_2}-{y_0}=\frac{1}{2}{x_1}{x_2}$,则y1=y2,∴k=0
此时直线AB:y=kx+a=a,则${y_0}=-\frac{1}{2}{x_1}{x_2}+{y_1}=-\frac{1}{2}•({-4a})+a=3a$,即Q(0,3a)
解答 解:抛物线C:x2=4y的焦点F(0,1),(1分)
设A(x1,y1),B(x2,y2),联立x2=4y与y=kx+a有x2-4kx-4a=0,
则△=16(k2+a)>0,且x1+x2=4k,x1•x2=-4a.(2分)
(Ⅰ)若直线l过焦点F,则a=1,则x1+x2=4k,x1•x2=-4.
由条件可知圆x2+(y-1)2=1圆心为F(0,1),半径为1,
由抛物线的定义有|AF|=y1+1,|BF|=y2+1,
则|AD|=|AF|-1=y1,|BE|=|BF|-1=y2,|AD|•|BE|=y1y2=(kx1+1)(kx2+1)=${k^2}{x_1}{x_2}+k({{x_1}+{x_2}})+1=-4{k^2}+4{k^2}+1=1$,
(或$|{AD}|•|{BE}|={y_1}{y_2}=\frac{x_1^2}{4}•\frac{x_1^2}{4}=\frac{{{{({{x_1}{x_2}})}^2}}}{16}=\frac{{{{({-4})}^2}}}{16}=1$)
即|AD|•|BE|为定值,定值为1.(5分)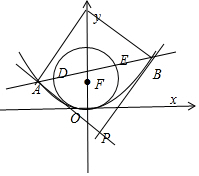
(Ⅱ)当直线l的斜率为0,且Q(0,3a)时APBQ为菱形.理由如下:(6分)
方法一:设A(x1,y1),B(x2,y2),Q(0,y0),由x2=4y有$y=\frac{1}{4}{x^2}$,则$y'=\frac{1}{2}x$,(7分)
若APBQ为菱形,则AQ∥BP,BQ∥AP,则${k_{AQ}}=\frac{{{y_1}-{y_0}}}{x_1}=\frac{1}{2}{x_2},{k_{BQ}}=\frac{{{y_2}-{y_0}}}{x_2}=\frac{1}{2}{x_1}$,
即${y_1}-{y_0}=\frac{1}{2}{x_1}{x_2},{y_2}-{y_0}=\frac{1}{2}{x_1}{x_2}$,
则y1=y2,∴k=0,∴$A({-2\sqrt{a},a}),B({2\sqrt{a},a})$,(9分)
则抛物线C在$A({-2\sqrt{a},a})$处的切线为$y-a=-\sqrt{a}({x+2\sqrt{a}})$,即$y=-\sqrt{a}x-a$…①
同理抛物线C在$B({2\sqrt{a},a})$处的切线为$y=\sqrt{a}x-a$…②(10分)
联立①②P(0,-a).(11分)
又AB的中点为R(0,a),所以Q(0,3a).(12分)
方法二:设A(x1,y1),B(x2,y2),Q(0,y0),由x2=4y有$y=\frac{1}{4}{x^2}$,则$y'=\frac{1}{2}x$,(7分)
若APBQ为菱形,则AQ∥BP,BQ∥AP,
则${k_{AQ}}=\frac{{{y_1}-{y_0}}}{x_1}=\frac{1}{2}{x_2},{k_{BQ}}=\frac{{{y_2}-{y_0}}}{x_2}=\frac{1}{2}{x_1}$,即${y_1}-{y_0}=\frac{1}{2}{x_1}{x_2},{y_2}-{y_0}=\frac{1}{2}{x_1}{x_2}$,
则y1=y2,∴k=0,(9分)
此时直线AB:y=kx+a=a,则${y_0}=-\frac{1}{2}{x_1}{x_2}+{y_1}=-\frac{1}{2}•({-4a})+a=3a$(11分)
所以Q(0,3a).(12分)
点评 本题考查了抛物线的方程、性质,抛物线的切线,考查了方程思想、转化思想,考查了运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
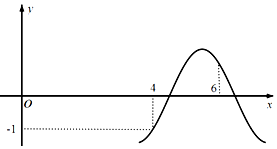
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com