
分析 (1)利用点在函数的图象上,推出递推关系式,然后求解数列的和.
(2)利用不等式恒成立,转化为函数的关系,通过二次函数的性质,以及数列的和得到不等式,求解k即可.
解答 解:(1)由题意,${a_{n+1}}=\frac{1}{3}{a_n}$,
得数列{an}为等比数列,
得${a_1}+\frac{1}{3}{a_1}+\frac{1}{9}{a_1}=\frac{13}{9}$,解得a1=1.
∴${a_n}={(\frac{1}{3})^{n-1}}$.${S_n}=\frac{{1-{{(\frac{1}{3})}^n}}}{{1-\frac{1}{3}}}=\frac{3}{2}[1-{(\frac{1}{3})^n}]$.
(2)$k{(-1)^n}a_n^2<{S_n}$(n∈N*)恒成立等价于$k{(-1)^n}{(\frac{1}{3})^{2(n-1)}}<\frac{1}{2}[3-{(\frac{1}{3})^{n-1}}]$(n∈N*)恒成立,
当n为奇数时,上述不等式左边恒为负数,右边恒为正数,所以对任意正整数k,不等式恒成立;
当n为偶数时,上述不等式等价于$2k{(\frac{1}{3})^{2(n-1)}}+{(\frac{1}{3})^{n-1}}-3<0$恒成立,
令${(\frac{1}{3})^{n-1}}=t$,有$0<t≤\frac{1}{3}$,
则①等价于2kt2+t-3<0在$0<t≤\frac{1}{3}$时恒成立,
因为k为正整数,二次函数y=2kt2+t-3的对称轴显然在y轴左侧,
所以当$0<t≤\frac{1}{3}$时,二次函数为增函数,
故只须$2k{(\frac{1}{3})^2}+\frac{1}{3}-3<0$,
解得0<k<12,k∈N*.{bn}是首项为b1=3,公差为d=-1的等差数列,所以前n项和${T_n}=3n+\frac{n(n-1)×(-1)}{2}$=$\frac{{-{n^2}+7n}}{2}$.
当n=3或4时,Tn取最大值为6.Tn>k有解?(Tn)max>k?k<6.
又0<k<12,k∈N*,
得0<k<6,k∈N*,
所以k的取值为1,2,3,4,5.
点评 本题考查数列与函数相结合,不等式的应用,函数的性质,考查转化思想以及计算能力.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{3}}]∪[{2,+∞}]$ | B. | $({-∞,-\frac{1}{3}}]∪[{\frac{1}{4},+∞})$ | C. | $({-∞,\frac{1}{4}}]∪[{\frac{9}{4},+∞})$ | D. | $({-∞,-\frac{1}{3}}]∪[{\frac{9}{4},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
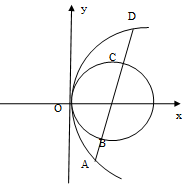 如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,
如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” | |
| B. | 若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c” | |
| C. | l是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β | |
| D. | 命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{8}^{4}$ | B. | C${\;}_{8}^{2}$ | C. | 24C${\;}_{8}^{4}$ | D. | 22C${\;}_{8}^{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com