
分析 根据新定义,[x]表示不超过x的最大整数,{x}=x-[x],需要分类讨论,根据条件得到x═a+$\frac{1}{a(a+1)}$,继而求出a的可能值,最后代入计算即可.
解答 解:显然,x不可能是整数,
否则由于{x}=0,方程[x]•{x}•<x>=1不可能成立.
设[x]=a,则{x}=x-a,x=a+1,
代入得a(x-a)(a+1)=1,
解得x=a+$\frac{1}{a(a+1)}$.
考虑到x∈[0,n+1],且[x]≠0,所以a=1,2,3,4,5,…,n,
故符合条件的解有n个,即m=n,
则x1+x2+…+xm=x1+x2+…+xn=$\frac{n(n+1)}{2}$+1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=$\frac{n(n+1)}{2}$+1-$\frac{1}{n+1}$=$\frac{n(n+1)}{2}$+$\frac{n}{n+1}$.
故答案为:$\frac{n(n+1)}{2}$+$\frac{n}{n+1}$.
点评 本题考查了函数的值,需要分类进行讨论,新定义一般需要认真读题,理解题意,灵活利用已知定义,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | (1,-l) | C. | (-l,1) | D. | (-l,-l) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
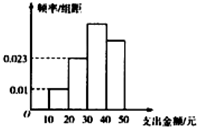 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com